
【题目】综合与实践
问题解决:
如图1,已知正方形![]() ,
,![]() ,把含
,把含![]() (
(![]() )的直角三角板的一个锐角顶点和点
)的直角三角板的一个锐角顶点和点![]() 重合,三角板和正方形的
重合,三角板和正方形的![]() ,
,![]() 两边分别相交于
两边分别相交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
探究发现:
(2)在图1的基础上,试探究![]() ,
,![]() ,
,![]() 有怎样的数量关系,请写出猜想,并给予证明.
有怎样的数量关系,请写出猜想,并给予证明.
类比延伸:
(3)如图2,若三角板和正方形![]() ,
,![]() 两边的延长线分别相交于
两边的延长线分别相交于![]() ,
,![]() 两点,请直接写出
两点,请直接写出![]() ,
,![]() ,
,![]() 存在的数量关系.
存在的数量关系.


【答案】(1)![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)直接利用勾股定理,即可求出AM的长度;
(2)延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .先证明
.先证明![]() ,得到
,得到![]() ,然后得到
,然后得到![]() ,再证明
,再证明![]() ,即可得到结论成立.
,即可得到结论成立.
(3)在CN上截取CE=AM,连接ME,先证明△BCE≌△ABM,然后得到△MBE为等腰直角三角形,再根据垂直平分线的性质,线段的和差关系,即可得到结论.
解:(1)∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
(2)猜想:![]() .
.
证明:延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.

在![]() 和
和![]() 中,
中,
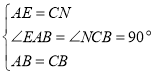 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)在CN上截取CE=AM,连接ME,

∵BC=AB,∠BAM=∠C=90°,
∴△BCE≌△BAM,
∴BE=BM,∠ABM=∠CBE,
∵∠MBN=45°,∠ABC=90°,
∴∠MBE=90°,△MBE为等腰直角三角形,
∴BN垂直ME,
∴BN为ME垂直平分线,
∴NM=NE.
∴CN-AM=CN-CE=NE=MN,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.比如在学习“同底数幂的乘法法则”过程中,利用有理数的乘方概念和乘法结合律,可由“特殊”抽象概括出“一般”,具体如下22×23=25,23×24=27,22×26=28…→2m2n=2m+n…→aman=am+n(m、n都是正整数)我们亦知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)请你根据上面的材料,用字母a、b、c归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式.
(2)请尝试说明(1)中关系式的正确性.
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:![]() ,精确到
,精确到![]() ,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_____,所抽查的学生人数为______.
的值为_____,所抽查的学生人数为______.
(2)求出平均睡眠时间为8小时的人数,并补全条形统计图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1800名,请你估计睡眠不足(少于8小时)的学生数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假降至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动. 活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). 大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 不获奖 |
圆心角 |
|
|
|
| _________ |
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆 一等奖:双肩背包一个
二等奖:洗衣液一桶 三等奖:抽纸一盒
根据以上信息,解答下列问题:
(1)求不获奖的扇形区域圆心角度数是多少?
(2)求获得双肩背包的概率是多少?
(3)甲顾客购物520元,求他获奖的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 中点,过点
中点,过点![]() 的直线分别与
的直线分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,则下列结论:
,则下列结论:
①![]() ,
,![]() ;
;
②![]() ;
;
③四边形![]() 是菱形;
是菱形;
④![]() .
.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举办“大爱镇江”征文活动,小明为此次活动设计了一个以三座山为背景的图标(如图),现用红、黄两种颜色对图标中的A、B、C三块三角形区域分别涂色,一块区域只涂一种颜色.

(1)请用树状图列出所有涂色的可能结果;
(2)求这三块三角形区域中所涂颜色是“两块黄色、一块红色”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com