Question

17．如图，E、F分别是AD和BC上的两点，EF将四边形ABCD分成两个边长为5cm的正方形，∠DEF=∠EFB=∠B=∠D=90°；点H是CD上一点且CH=lcm，点P从点H出发，沿HD以lcm/s的速度运动，同时点Q从点A出发，沿A→B→C以5cm/s的速度运动．任意一点先到达终点即停止运动；连结EP、EQ．
（1）如图1，点Q在AB上运动，连结QF，当t=$\frac{1}{4}$时，QF∥EP；
（2）如图2，若QE⊥EP，求出t的值；
（3）试探究：当t为何值时，△EPD的面积等于△EQF面积的$\frac{7}{10}$．

Answer 1

分析 （1）假设EP∥FQ，得到∠PEF=∠EFQ，由等角的余角相等，得∠QFB=∠DEP，通过正切关系，得到BQ与PD关系，求出t；
（2）通过△QEF≌△PED，得到FQ与PD间关系，进而求出t的值；
（3）分类讨论：①当点Q在AB上时；②当点Q在BF上时，③当点Q在CF上时，分别求出t．

解答 解：（1）由题意知：ED=FB=5cm，∠D=∠B=∠DEF=∠EFB=90°，
若EP∥FQ时，∠PEF=∠EFQ，
∴∠DEP=∠DEF-∠PEF=∠EFB-∠EFQ=∠QFB，
∴tan∠QFB=$\frac{QB}{BF}=\frac{DP}{DE}$=tan∠DEP，
所以BQ=DP．
∵BQ=5-5t，DP=DC-CH-PH=5-1-t=4-t，
∴5-5t=4-t，
∴t=$\frac{1}{4}$；
答案：$\frac{1}{4}$．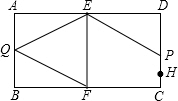

（2）如图所示，若QE⊥EP，则∠QEP+∠FEP=90°，
又∵∠DEP+∠PEF=90°，
∴∠QEF=∠DEP
在△QEF和△PED中，$\left\{\begin{array}{l}{∠QEF=∠DEP}\\{EF=ED}\\{∠D=EFQ}\end{array}\right.$

∴△QEF≌△PED，
∴QF=DP．
∵FQ=10-5t，DP=4-t，
∴10-5t=4-t，
∴t=$\frac{3}{2}$．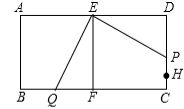

（3）①如图所示，过Q做QM⊥EF，垂足为M．
由于四边形ABFE是正方形，所以QM=AE=5cm．
当0＜t≤1时，S_△EQF=$\frac{1}{2}$EF×QM=$\frac{1}{2}×5×5=12.5$，S_△EPD=$\frac{1}{2}$ED×DP=$\frac{1}{2}×5×（4-t）$，
当$\frac{7}{10}$S_△EQF=S_△EPD时，即$\frac{7}{10}$×12.5=$\frac{1}{2}$×5×（4-t），
解得，t=0.5；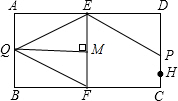

②当1＜t≤2时，S_△EQF=$\frac{1}{2}$×EF×FQ=2.5FQ，S_△EPD=$\frac{1}{2}$ED×DP=$\frac{1}{2}$×5×（4-t），
∵FQ=10-5t，
∴$\frac{7}{10}$×2.5（10-5t）=$\frac{1}{2}$×5×（4-t），
解得：t=$\frac{6}{5}$；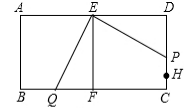

③当2＜t≤3时，S_△EQF=$\frac{1}{2}$FQ×EF=2.5（5t-10），S_△EPD=$\frac{1}{2}$ED×DP=$\frac{1}{2}$×5×（4-t），
∴$\frac{7}{10}$×2.5×（5t-10）=2.5（4-t），
解得：t=$\frac{22}{9}$．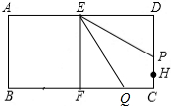

点评 点评：本题是一个比较基础的四边形综合题，主要考察了正方形的性质和三角形的面积计算．本题重点考察了分类讨论的思想，确定点Q所在的位置，是解决本题的关键．