
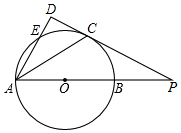
 如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.
如图,AB为⊙O的直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE交AE的延长线于D点,直线CD与射线AB交于P点.分析 (1)连接OC,根据角平分线的定义、等腰三角形的性质证明OC∥AD,得到∠OCP=∠D=90°,根据切线的判定定理证明;
(2)连接BC,根据勾股定理求出AD,根据相似三角形的性质计算即可.
解答 (1)证明: 连接OC,
连接OC,
∵AC是∠EAB的平分线,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∴∠OCP=∠D=90°,
∴DC为⊙O切线;
(2)解:连接BC,
∵∠D=90°,DC=1,AC=$\sqrt{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=2,
∵∠OAC=∠OCA,∠ACB=∠D,
∴△ADC∽△ACB,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,即AC2=AD•AB,
则AB=$\frac{A{C}^{2}}{AD}$=$\frac{5}{2}$,
∴⊙O的半径长为$\frac{5}{4}$.
点评 本题考查的是切线的判定、相似三角形的判定和性质、勾股定理的应用,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△A1OB1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等腰三角形ABC的底角为30°,以腰BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC的底角为30°,以腰BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | -4 | -4 | 0 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
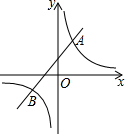 如图,已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
如图,已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com