
【题目】如图,C为线段AB上一点,D在线段AC上,且AD=![]() AC,E为BC的中点.
AC,E为BC的中点.
(1)若AC=6,BE=1,求线段AB、DE的长;
(2)试说明:AB+BD=4DE.
![]()
【答案】(1)AB=8,DE=3; (2)理由见解析.
【解析】(1)根据AD=![]() AC,E为BC的中点,可求出DC和BC的长,再根据AB=AC+BC,DE=DC+CE,即可求出答案;
AC,E为BC的中点,可求出DC和BC的长,再根据AB=AC+BC,DE=DC+CE,即可求出答案;
(2)根据AD=![]() AC,E为BC的中点,将AB+BD转化为DC与CE的和的形式,即可证明.
AC,E为BC的中点,将AB+BD转化为DC与CE的和的形式,即可证明.
解:(1)∵E为BC的中点,且BE=1,
∴BC=2BE=2,
∴AB=AC+BC=6+2=8,
∵AD=![]() AC,且AC=6,
AC,且AC=6,
∴CD=![]() AC=2,
AC=2,
∵E为BC的中点,且BE=1,
∴CE=BE=1,
∴DE=DC+CE=2+1=3;
(2)∵AB=AC+BC,BD=BC+CD,
∴AB+BD=AC+BC+BC+CD,
∵AD=![]() AC,E为BC的中点,
AC,E为BC的中点,
∴AC=3CD,BC=2CE,
∴AB+BD=3CD+2CE+2CE+CD=4CD+4CE=4(CD+CE)=4DE.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,解答下列问题: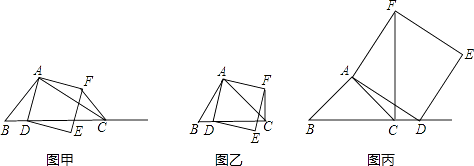
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系是什么?写出它们之间的数量关系.
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,请证明?
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?直接写出条件,不需要证明.
(3)若AC=4 ![]() ,BC=3,在(2)的条件下,求△ABC中AB边上的高.
,BC=3,在(2)的条件下,求△ABC中AB边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=__.
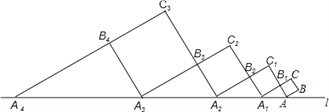
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点C为线段AB上一点,AB=12,AC=8,点D为直线AB上一点,M、N分别是AB、CD的中点,若MN=10,则线段AD的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器按成本价提高30%后标价,再打八折销售,售价为2080元.设该电器的成本价为x元,由题意,下面所列方程正确的是( )
A.80%(1+30%)x=2080
B.30%80%x=2080
C.2080×30%×80%=x
D.30%x=2080×80%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司拥有20辆汽车。据统计,当每辆车的日租金为400元时,可全部租出;当辆车的日租金每增加50元时,未租出的车将增加1辆;公司平均每日的各项支出共4800元。设公司每日租出![]() 辆车,日收益为
辆车,日收益为![]() 元,(日收益=日租金收入-平均每日各项支出)。
元,(日收益=日租金收入-平均每日各项支出)。
(1)公司每日租出![]() 辆车时,每辆车的日租金为 元(用含
辆车时,每辆车的日租金为 元(用含![]() 的代数式表示);
的代数式表示);
(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?
(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据 1,2,3,4,5 的方差与下列哪组数据的方差相同的是( )
A. 2,4,6,8,10 B. 10,20,30,40,50
C. 11,12,13,14,15 D. 11,22,33,44,55
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: ![]() )
)
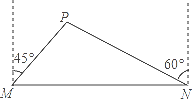
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com