练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．下列计算中，正确的是（　　）
    A．3a+2b=5abB．7ab-4ba=0C．4x2y-3xy2=x2yD．3x2+5x2=8x2

    分析 根据合并同类项系数相加字母及指数不变，可得答案．

    解答 解：A、不是同类项不能合并，故A错误；
    B、合并同类项系数相加字母及指数不变，故B错误；
    C、不是同类项不能合并，故C错误；
    D、合并同类项系数相加字母及指数不变，故D正确；
    故选：D．

    点评 本题考查了合并同类项，注意合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

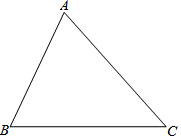    18．如图，在某城区地图上，有一块△ABC区域，市政规划要把△ABC区域划分成三个三角形小区域，使任何两个区域都相邻，并且使划分的三个小区域面积彼此相等．请你探究后，把符合题意的示意图画在图中，并说明所画的线是什么线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

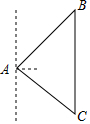    19．随着南海局势的升级，中国政府决定在黄岩岛填海造陆，修建机场，设立雷达塔．某日，在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域，且以30海里/时的速度往正南方向航行，我方与其进行多次无线电沟通无果后，这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处，与此同时我方立即通知（通知时间忽略不计）与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截，其中海警船位于与A相距100海里的D处．
    （1）求点D到直线BC的距离；
    （2）若海警船航行速度为40海里时，可侦测半径为25海里，问海警船最快几小时可以侦测到菲律宾渔船？（参考数据：sin53°≈$\frac{4}{5}$，cos53°≈$\frac{3}{5}$，tan53°≈$\frac{4}{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=12，点D是AB的中点，动点E从点A出发，以每秒一个单位的速度沿折线A-C-B向终点B运动，连接DE，以DE为直角边，点E为直线顶点向右侧作等腰直角△DEF，设点E的运动时间为t秒
    （1）直接写出线段AC和BC的长：AC=6$\sqrt{3}$，BC=6；
    （2）若DF∥AC时，
    ①求t的值；
    ③若DF交BC于点H，EF交BC于点G，则四边形DEGH的面积是18$\sqrt{3}$-$\frac{45}{2}$（直接写答案）；
    （3）当点F落在△ABC三边所在的直线上时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知AB=AD，BC=DC．求证：AC平分∠BAD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，点B、E、C、F在同一条直线上，∠A=∠D，AB∥DE，BE=CF，求证：AC∥DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

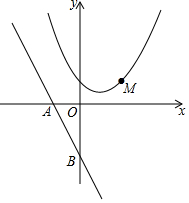    20．直线y=-$\frac{4}{3}$x-4与x轴交于点A，与y轴交于点B，抛物线y=x2-4x+5上的一点M（3，2）．
    （1）求点M到直线AB的距离；
    （2）抛物线上是否存在点P，使得△PAB的面积最小？若存在，求出点P的坐标及△PAB面积的最小值；不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．平面直角坐标系中，A（3，0），B（2，2），P，Q两点在直线x=1上，P在Q的上面，PQ=1，则四边形ABPQ的周长最小值为$\sqrt{5}$+$\sqrt{10}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知α+β=90°，且sinα=$\frac{1}{5}$，则sinβ=$\frac{2\sqrt{6}}{5}$．

    查看答案和解析>>

    同步练习册答案