
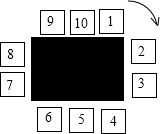
 ��ͼ����һ��������Χ������10�����ӣ���˳ʱ�뷽���Ϊ1��10�ţ�С����1��������Ͷ��һ�ź�����������Ӱ�˳ʱ�뷽�����ߣ�ÿ����һ�����Ӿ������й���Ͷ��һ����
��ͼ����һ��������Χ������10�����ӣ���˳ʱ�뷽���Ϊ1��10�ţ�С����1��������Ͷ��һ�ź�����������Ӱ�˳ʱ�뷽�����ߣ�ÿ����һ�����Ӿ������й���Ͷ��һ�������� �����һ�㣬̽�����ɺ��жϣ�
��� �⣺��1Ȧ�����4�����ӵ��Ǻ���
��2Ȧ�����4�����ӵ��ǻ���
��3Ȧ�����4�����ӵ�������
��4Ȧ�����4�����ӵ��Ǻ���
��
�۲췢��4�����ӵ����ǰ��պ졢�ơ��̵Ĺ��ɱ仯�ģ�
��������10Ȧ�����4�������ں����������ĸ����ֱ���4��3��3��
�ʴ�Ϊ4��3��3��
���� ���⿼����������֤����������Ŀ��֪ʶ������Ĺؼ���ѧ������һ���̽�����������ֹ��ɣ����ù��ɽ�����⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
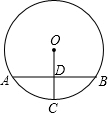 ��ͼ��AB�ǡ�O���ң��뾶OC��AB�ڵ�D����AB=8cm��OC=5cm����DC�ij���
��ͼ��AB�ǡ�O���ң��뾶OC��AB�ڵ�D����AB=8cm��OC=5cm����DC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
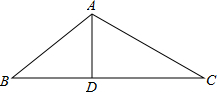 ��ͼ��DΪ��ABC��BC���ϵ�һ�㣬AB=10��AD=6��DC=2AD��BD=$\frac{2}{3}$DC��
��ͼ��DΪ��ABC��BC���ϵ�һ�㣬AB=10��AD=6��DC=2AD��BD=$\frac{2}{3}$DC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
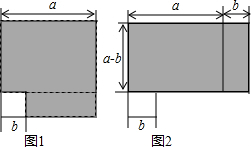 ��ͼ��������Ӱ��������ֲ�ͬ�ļ��㷽������֤�˳�����ѧ���ĸ���ʽ����a2-b2=��a+b����a-b����
��ͼ��������Ӱ��������ֲ�ͬ�ļ��㷽������֤�˳�����ѧ���ĸ���ʽ����a2-b2=��a+b����a-b�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com