
 ,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是( )
,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是( ) ,4)
,4)科目:初中数学 来源: 题型:
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-反比例函数的应用(带解析) 题型:解答题
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
第二学习小组发现:如图(2),点P是反比例函数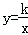 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
请利用上述结论解决下列问题:
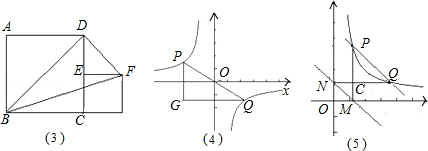
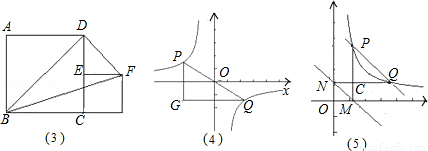
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则S△BDF= 2 .
(2)如图(4),点P、Q在反比例函数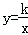 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= 2 ,k= ﹣4 .
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= 2 ,k= ﹣4 .
(3)如图(5)点P、Q是第一象限的点,且在反比例函数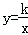 图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-反比例函数的应用(解析版) 题型:解答题
九年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2,则S△ABC=S△ABD;反之亦成立.
第二学习小组发现:如图(2),点P是反比例函数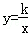 上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
上任意一点,过点P作x轴、y轴的垂线,垂足为M、N,则矩形OMPN的面积为定值|k|.
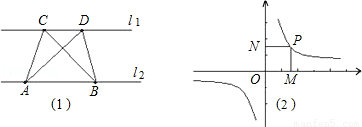
请利用上述结论解决下列问题:
(1)如图(3),四边形ABCD、与四边形CEFG都是正方形点E在CD上,正方形ABCD边长为2,则S△BDF= 2 .
(2)如图(4),点P、Q在反比例函数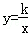 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= 2 ,k= ﹣4 .
图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= 2 ,k= ﹣4 .
(3)如图(5)点P、Q是第一象限的点,且在反比例函数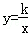 图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
图象上,过点P作x轴垂线,过点Q作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 ,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是
,4)五个点在同一个反比例函数的图象上,后来经检查发现其中有一个点不在,这个点是(2,-3)
(-2,3)
(-2,-3)
( ,4)
,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com