
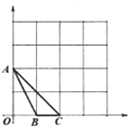
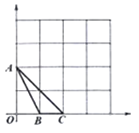
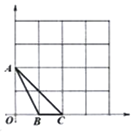
【题目】 如图,在矩形ABCD中,AB=6,BC=10,P是AD边上一动点(不含端点A,D),连接PC,E是AB边上一点,设BE=a,若存在唯一点P,使∠EPC=90°,则a的值是( )
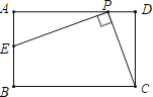
A.![]() B.
B.![]() C.3D.6
C.3D.6
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线l1:y=![]() x2+c,当其函数值y=1时,只有一个自变量x的值与其对应
x2+c,当其函数值y=1时,只有一个自变量x的值与其对应
(1)求c的值;
(2)将抛物线l1经过平移得到抛物线l2:y=![]() (x﹣p)2﹣1.
(x﹣p)2﹣1.
①若抛物线l2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,记△ABC的外心为P,当﹣1≤p≤![]() 时,求点P的纵坐标的取值范围;
时,求点P的纵坐标的取值范围;
②当0≤x≤2时,对于抛物线l1上任意点E,抛物线l2上总存在点F,使得点E、F纵坐标相等,求p的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.
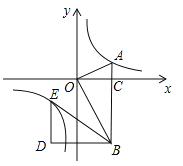
(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
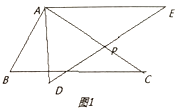
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕顶点
绕顶点![]() 逆时针旋转时,当
逆时针旋转时,当![]() 时,设
时,设![]() 与
与![]() 于
于![]() ,证明:
,证明:![]() 是等边三角形;
是等边三角形;
(2)如图1,在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕顶点
绕顶点![]() 逆时针旋转
逆时针旋转![]() 多少度时,
多少度时,![]() ,使得
,使得![]() 的顶点
的顶点![]() 落在
落在![]() 上?
上?
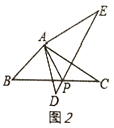
(3)当直角三角形变为一般三角形时,如图2,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可以得到
,可以得到![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列![]() (边长为1)的网格中,已知
(边长为1)的网格中,已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 在格点上,请分别按不同要求在网格中描出一个格点
在格点上,请分别按不同要求在网格中描出一个格点![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(1)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后所得的三角形,点
,画出旋转后所得的三角形,点![]() 旋转后落点为
旋转后落点为![]() .
.
(2)经过![]() ,
,![]() ,
,![]() 三点有一条抛物线,请找到点
三点有一条抛物线,请找到点![]() ,使点
,使点![]() 也落在这条抛物线上.
也落在这条抛物线上.
(3)经过![]() ,
,![]() ,
,![]() 三点有一个圆,请找到一个横坐标为2的点
三点有一个圆,请找到一个横坐标为2的点![]() ,使点
,使点![]() 也落在这个圆上.
也落在这个圆上.
(1)点![]() 的坐标为( , )
的坐标为( , )
(2)点![]() 的坐标为( , )/span>
的坐标为( , )/span>
(3)点![]() 的坐标为( , )
的坐标为( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知:直线y=-x-4分别交x、y轴于A、C两点,点B为线段AC的中点,抛物线y=ax2+bx经过A、B两点,
(1)求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,连结AD、CD,问在抛物线上是否存在点P,使S△ACP=2S△ACD?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若E为⊙D上一动点(不与A、O重合),连结AE、OE,问在x轴上是否存在点Q,使∠ACQ:∠AEO=2:3?若存在,请求出所有满足条件的点Q的坐标;若不存在,请说明理由.
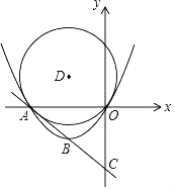
查看答案和解析>>
科目:初中数学 来源: 题型:
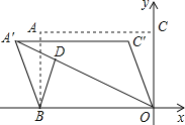
【题目】如图,在平面直角坐标系中,矩形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,AC长为![]() ,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=
,若将边AC平移至A'C'处,此时A'坐标为(-4,2),分别连接A'B,C'O,反比例函数y=![]() 的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
的图象与四边形A'BOC'对角线A'O交于D点,连接BD,则当BD取得最小值时,k的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨。梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°, AD=3m。
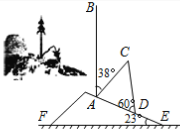
(1)求∠DAC的度数;
(2)求这棵大树折断前的高度。(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com