练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    探究下列问题：

    （1）请你用火柴棒搭一个四边形，并且使任意三边不能构成三角形，则至少需要几根火柴棒？画出符合条件的这个四边形；

    （2）如果搭一个五边形呢？

     

    答案：
    解析：

    		（1）1+1+2+3=7根火柴棒  （2）1+1+2+3+5=12

     


    提示：

    		三角形的构成条件

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

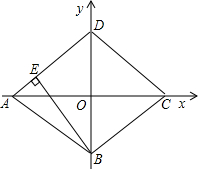    精英家教网已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为（4，0），（0，3）．现有两动点P，Q分别从A，C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒．
    （1）填空：菱形ABCD的边长是
     
    、面积是
     
    、高BE的长是
     
    ；
    （2）探究下列问题：
    ①若点P的速度为每秒1个单位，点Q的速度为每秒2个单位．当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；
    ②若点P的速度为每秒1个单位，点Q的速度变为每秒k个单位，在运动过程中，任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形．请探究当t=4秒时的情形，并求出k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

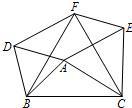    18、如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE、等边△BCF．
    （1）求证：四边形DAEF是平行四边形；
    （2）探究下列问题：（只填满足的条件，不需证明）
    ①当△ABC满足
    ∠BAC=150°
    条件时，四边形DAEF是矩形；
    ②当△ABC满足
    AB=AC≠BC
    条件时，四边形DAEF是菱形；
    ③当△ABC满足
    ∠BAC=60°
    条件时，以D、A、E、F为顶点的四边形不存在．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD．探究下列问题：
    （1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD=
     
    ；
    （2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD=
     
    ；
    （3）如图3，当∠ACB变化，且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将两个大小一样的正方形ABCD和正方形CDEF如图放置，点B、C、F在同一直线上，BF=12，再将一直角三角板的直角顶点放置在D点上，DP交AB于点M，DQ交BF于点N．
    （1）求证：△DBM≌△DFN；
    （2）将三角板DPQ的直角顶点绕点D旋转时，四边形DMBN的面积是否变化？如果不变，请简要说明理由并求出它的面积；
    （3）分别延长正方形的边CB和边EF，使它们的延长线分别与直角三角板的两边DP、DQ（或它们的延长线）交于点G和点H，试探究下列问题：
    ①线段BG与FH相等吗？说明你的理由；
    ②当线段FN的长是方程x2+x-12=0的一根时，试求出
    NGNH
    的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，在△ABC中，AD平分∠BAC，AE⊥BC，垂足为E．
    （1）若∠B=35°，∠C=75°，求∠DAE的度数；
    （2）若∠B=α，∠C=β，且0°＜α＜β＜90°，试探究下列问题：
    ①∠DAE=
    1
    2
    β-
    1
    2
    α
    1
    2
    β-
    1
    2
    α
    （用含α、β的代数式表示）；
    ②若点P为射线AD上任意一点（除点A、点D外），过点P作PQ⊥BC，垂足为Q（请在图2、图3中将图形补充完整），请用含α、β的代数式表示∠DPQ并说明理由．

    查看答案和解析>>

    同步练习册答案