
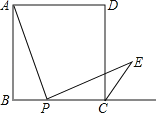
【题目】如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B,C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E,设BP=x,△PCE面积为y,则y与x的函数关系式是_____.
【答案】![]() .
.
【解析】
过E作EH⊥BC于H,证明△BAP∽△HPE,求出EH=x,所以y=![]() CPEH=
CPEH=![]() (4-x)x=-
(4-x)x=-![]() x2+2x,
x2+2x,
过E作EH⊥BC于H,
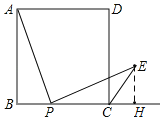
∵四边形ABCD是正方形,
∴∠DCH=90°,
∵CE平分∠DCH,
∴∠ECH=![]() ∠DCH=45°,
∠DCH=45°,
∵∠EHC=90°,
∴∠ECH=∠CEH=45°,
∴EH=CH,
∵四边形ABCD是正方形,AP⊥EP,
∴∠B=∠H=∠APE=90°,
∴∠BAP+∠APB=90°,∠APB+∠EPH=90°,
∴∠BAP=∠EPH,
∵∠B=∠EHP=90°,
∴△BAP∽△HPE,
∴![]() ,
,
即![]() ,
,
∴EH=x,
∴y=![]() CPEH=
CPEH=![]() (4﹣x)x=﹣
(4﹣x)x=﹣![]() x2+2x,
x2+2x,
故答案为:y=﹣![]() x2+2x.
x2+2x.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
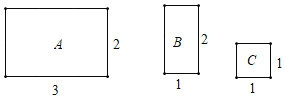
【题目】如图,A型、B型、C型三张矩形卡片的边长如图所示,将三张矩形卡片分别放入三个信封中,三个信封的外表完全相同;
(1)从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为______;
(2)先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
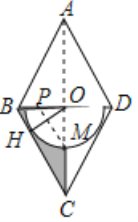
【题目】如图,在菱形ABCD中,连结BD、AC交于点O,过点O作![]() 于点H,以点O为圆心,OH为半径的半圆交AC于点M.
于点H,以点O为圆心,OH为半径的半圆交AC于点M.
①求证:DC是⊙O的切线.
②若![]() 且
且![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
③在②的条件下,P是线段BD上的一动点,当PD为何值时,![]() 的值最小,并求出最小值.
的值最小,并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 、点
、点![]() .
.
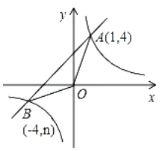
(1)求一次函数和反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)直接写出一次函数值大于反比例函数值的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
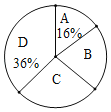
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了 个参赛学生的成绩;
(2)表1中![]() ;
;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A |
| a |
B |
| 10 |
C |
| 14 |
D |
| 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
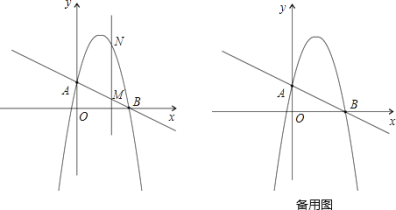
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com