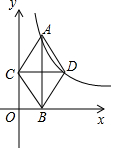
如图.在直角坐标系中.点A在函数y=$\frac{4}{x}$的图象上.AB⊥x轴于点B.AB的垂直平分线与y轴交于点C.与函数y=$\frac{4}{x}$的图象交于点D.连结AC.CB.BD.DA.则四边形ACBD的面积等于( )A．2B．2$\sqrt{3}$C．4D．4$\sqrt{3}$ 题目和参考答案——青夏教育精英家教网—

18．

如图，在直角坐标系中，点A在函数y=$\frac{4}{x}$（x＞0）的图象上，AB⊥x轴于点B，AB的垂直平分线与y轴交于点C，与函数y=$\frac{4}{x}$（x＞0）的图象交于点D，连结AC，CB，BD，DA，则四边形ACBD的面积等于（　　）

A．

B．

2$\sqrt{3}$

C．

D．

4$\sqrt{3}$

分析设A（a，$\frac{4}{a}$），可求出D（2a，$\frac{2}{a}$），由于对角线垂直，计算对角线乘积的一半即可．

解答解：设A（a，$\frac{4}{a}$），可求出D（2a，$\frac{2}{a}$），
∵AB⊥CD，
∴S_{四边形ACBD}=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×2a×$\frac{4}{a}$=4，
故选C．

点评本题主要考查了反比例函数系数k的几何意义以及线段垂直平分线的性质，解题的关键是设出点A和点B的坐标．

练习册系列答案

8年沉淀1年突破单元同步夺冠卷系列答案

导学与测试系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

8．

某电视台的一档娱乐性节目中，在游戏PK环节，为了随机分选游戏双方的组员，主持人设计了以下游戏：用不透明的白布包住三根颜色长短相同的细绳AA₁、BB₁、CC₁，只露出它们的头和尾（如图所示），由甲、乙两位嘉宾分别从白布两端各选一根细绳，并拉出，若两人选中同一根细绳，则两人同队，否则互为反方队员．
（1）若甲嘉宾从中任意选择一根细绳拉出，求他恰好抽出细绳AA₁的概率；
（2）请用画树状图法或列表法，求甲、乙两位嘉宾能分为同队的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．抛物线y=ax²+bx+3交x轴于点A（-3，0）和点B（1，0），交y轴于点C．
（1）求抛物线的函数表达式及抛物线的对称轴；
（2）如图a，点P是抛物线上第二象限内的一动点，若以AP，AO为邻边的平行四边形第四个顶点恰好落在抛物线上，求出此时点P的坐标；
（3）如图b，点D是抛物线上第二象限内的一动点，过点O，D的直线y=kx交AC于点E，若S_△CDE：S_△CEO=2：3，求k的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．如图1，在△ABC中，∠A=30°，点P从点A出发以2cm/s的速度沿折线A-C-B运动，点Q从点A出发以a（cm/s）的速度沿AB运动，P，Q两点同时出发，当某一点运动到点B时，两点同时停止运动．设运动时间为x（s），△APQ的面积为y（cm²），y关于x的函数图象由C₁，C₂两段组成，如图2所示．

（1）求a的值；
（2）求图2中图象C₂段的函数表达式；
（3）当点P运动到线段BC上某一段时△APQ的面积，大于当点P在线段AC上任意一点时△APQ的面积，求x的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．如图1，将△ABC纸片沿中位线EH折叠，使点A对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，HG折叠，折叠后的三个三角形拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．

（1）将?ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段AE，GF；S_矩形AEFG：S_?ABCD=1：2．
（2）?ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF=5，EH=12，求AD的长；
（3）如图4，四边形ABCD纸片满足AD∥BC，AD＜BC，AB⊥BC，AB=8，CD=10，小明把该纸片折叠，得到叠合正方形，请你帮助画出叠合正方形的示意图，并求出AD、BC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

3．如图，从边长为（a+3）的正方形纸片中剪去一个边长为3的正方形，剩余部分沿虚线又剪拼成一个如图所示的长方形（不重叠无缝隙），则拼成的长方形的另一边长是a+6．