
分析 根据抛物线的解析式找出抛物线的顶点坐标,再根据该抛物线的顶点在y轴的正半轴上,即可得出关于m的一元二次方程以及一元一次不等式,解方程及不等式即可得出结论.
解答 解:∵抛物线的解析式为y=5x2+(m2-4)x+1-m,
∴抛物线的顶点坐标为(-$\frac{{m}^{2}-4}{10}$,$\frac{20×(1-m)-({m}^{2}-4)^{2}}{20}$),
∵抛物线y=5x2+(m2-4)x+1-m的顶点在y轴的正半轴上,
∴$\left\{\begin{array}{l}{-\frac{{m}^{2}-4}{10}=0}\\{\frac{20×(1-m)-({m}^{2}-4)^{2}}{20}>0}\end{array}\right.$,
解得:m=-2.
点评 本题考查了二次函数的性质,牢记二次函数的顶点坐标是解题的关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
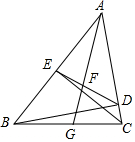 在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D,E,联结ED,∠BAC的平分线交ED于点F,交BC于点G,求证:AF:AG=ED:BC.
在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D,E,联结ED,∠BAC的平分线交ED于点F,交BC于点G,求证:AF:AG=ED:BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
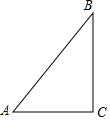 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,r为半径画⊙C,请根据下列条件,求半径r的值或取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com