Question

问题情境：如图1，直角三角板ABC中，∠C＝90°，AC＝BC，将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点。
问题探究：（1）在旋转过程中，
①如图2，当AD＝BD时，线段DP、DQ有何数量关系？并说明理由。
②如图3，当AD＝2BD时，线段DP、DQ有何数量关系？并说明理由。
③根据你对①、②的探究结果，试写出当AD＝nBD时，DP、DQ满足的数量关系为_______________（直接写出结论，不必证明）
（2）当AD＝BD时，若AB＝20，连接PQ，设△DPQ的面积为S，在旋转过程中，S是否存在最小值或最大值？若存在，求出最小值或最大值；若不存在，请说明理由。

图1              图2                 图3

Answer 1

（1）① DP=DQ  ②DP=2DQ ③DP="nDQ" （2）当DP⊥AC时，x最小，最小值是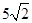，此时，S有最小值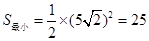，    当点P与点A重合时，x最大，最大值是10，此时，S有最大值，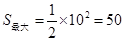

解析试题分析：此题主要考查了等腰直角三角形的性质和相似三角形的判定和性质以及二次函数最值求出等知识，熟练利用相似三角形的性质得出对应边关系是解题关键．
（1）①首先利用等腰直角三角形的性质得出△ADP≌△CDQ（ASA），即可得出答案；
②首先得出△DPM∽△DQN，则 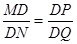 ，求出△AMD∽△BND，进而得出答案.
③根据已知得出Rt△DNP∽Rt△DMQ，则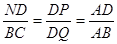 ，则AD=nBD，求出即可；
（2）当DP⊥AC时，x最小，最小值是5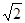 .此时，S有最小值；当点P与点A重合时，x最大，最大值为10，分别求出即可．
试题解析：（1）①DP＝DQ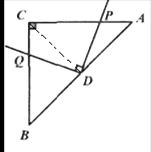     

理由：连接CD，
∵AD=BD，△ABC是等腰直角三角形，
∴AD=CD，∠A＝∠DCQ，∠ADC＝90°，∴∠ADP＋∠PDC＝∠CDQ＋∠PDC＝90°，
∴∠ADP＝∠CDQ，∴△ADP≌△CDQ，∴DP=DQ.
② DP=" 2DQ" 。           
理由：如图，过点D作DM⊥AC、DN⊥BC，垂足分别为M、N，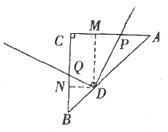

∴∠DMP＝∠DNQ＝90°，∠MDP＝∠NDQ，
∴△DPM∽△DQN，∴DM:DN="DP:DQ" 。
∵∠AMD＝∠DNB＝90°，∠A＝∠B，
∴△AMD∽△BND，∴AD:BD=DM:DN。
∴DP:DQ=AD:BD=2BD:BD=2:1，
∴DP=2DQ。                 
③DP=NQ。                 
（2）存在，设DQ=x，由（1）①知DP=x，
∴S=1／2xx=1／2x²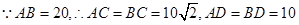
，
当DP⊥AC时，x最小，最小值是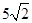，此时，S有最小值，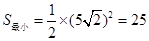  
当点P与点A重合时，x最大，最大值是10，此时，S有最大值，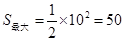
考点：几何变换综合题．