
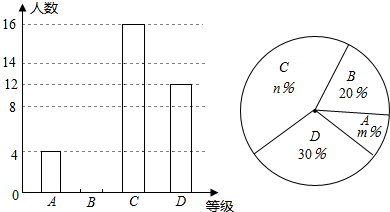
| A. | 参加演讲比赛学生共40人 | |
| B. | 扇形统计图中m=10,n=40 | |
| C. | 学校欲从获A等级的学生中随机选取2人参加市级比赛,选中A等级的小明的概率为$\frac{1}{2}$ | |
| D. | C等级所对应的圆心角为120度 |
分析 根据D等级有12人,所占的百分比是30%即可求得总人数,然后根据百分比的意义即可求得m和n的值,利用列举法求得选中A等级的小明的概率;利用360°乘以对应的百分比即可求得C等级所对应的圆心角度数.
解答 解:A、参加演讲比赛学生共有12÷30%=40(人),故命题正确;
B、m%=$\frac{4}{40}$×100=10%,则m=10,
n%=$\frac{16}{40}$×100%=40%,则n=40,故命题正确;
C、用a表示小明,用b、c、d表示另外三名同学.
则选中小明的概率是:$\frac{6}{12}$=$\frac{1}{2}$,故命题正确;
D、C等级所对应的圆心角为360°×40%=144°,则命题错误.
故选D.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
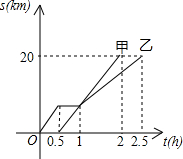 甲乙两同学在假日期间,义务担任“城市文明宣传员”.两人都从A地出发,骑自行车沿同一条路线宣传,均行驶到B地.他们离出发地距离S(km)与行驶时间t(h)之间的函数关系的图象如图所示.
甲乙两同学在假日期间,义务担任“城市文明宣传员”.两人都从A地出发,骑自行车沿同一条路线宣传,均行驶到B地.他们离出发地距离S(km)与行驶时间t(h)之间的函数关系的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
如图,点O是等边三角形ABC内一点,已知∠AOB=115°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
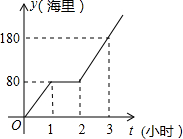 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则Cn的坐标是( )| A. | (-$\sqrt{3}$×4n,4n) | B. | (-$\sqrt{3}$×4n-1,4n-1) | C. | (-$\sqrt{3}$×4n-1,4n) | D. | (-$\sqrt{3}$×4n,4n-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com