
【题目】如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
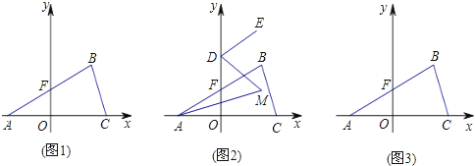
(1)求点A、B的坐标.
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图2,求∠AMD的度数.
(3)如图3,
①求点F的坐标;
②点P为坐标轴上一点,若△ABP的三角形和△ABC的面积相等?若存在,求出P点坐标.
【答案】(1)A(-3,0),B(3,3);(2)∠AMD=45°;(3)①F点坐标为(0,![]() );②满足条件的P点坐标为(0,5);(0,-2);(-10,0),(4,0).
);②满足条件的P点坐标为(0,5);(0,-2);(-10,0),(4,0).
【解析】
(1)根据非负数的性质得a+b=0,a-b+6=0,然后解方程组求出a和b即可得到点A和B的坐标;
(2)由AB∥DE得∠ODE+∠DFB=180°,而∠DFB=∠AFO=90°-∠FAO,所以∠ODE+90°-∠FAO=180°,再根据角平分线定义得∠OAN=![]() ∠FAO,∠NDM=
∠FAO,∠NDM=![]() ∠ODE,则∠NDM-∠OAN=45°,得∠NDM+∠DNM=135°,即可求出∠NMD=45°;
∠ODE,则∠NDM-∠OAN=45°,得∠NDM+∠DNM=135°,即可求出∠NMD=45°;
(3)①连结OB,如图3,设F(0,t),根据△AOF的面积+△BOF的面积=△AOB的面积,则可得到F点坐标为(0,![]() );
);
②先计算△ABC的面积=![]() ,分类讨论:当P点在y轴上时,设P(0,y),利用△ABP的三角形=△APF的面积+△BPF的面积,此时P点坐标为(0,5)或(0,-2);当P点在x轴上时,设P(x,0),求出此时P点坐标.
,分类讨论:当P点在y轴上时,设P(0,y),利用△ABP的三角形=△APF的面积+△BPF的面积,此时P点坐标为(0,5)或(0,-2);当P点在x轴上时,设P(x,0),求出此时P点坐标.
解:(1)∵(a+b)2+|a-b+6|=0,
∴a+b=0,a-b+6=0,
∴a=-3,b=3,
∴A(-3,0),B(3,3);
(2)如图2,

∵AB∥DE,
∴∠ODE+∠DFB=180°,
而∠DFB=∠AFO=90°-∠FAO,
∴∠ODE+90°-∠FAO=180°,
∵AM,DM分别平分∠CAB,∠ODE,
∴∠OAN=![]() ∠FAO,∠NDM=
∠FAO,∠NDM=![]() ∠ODE,
∠ODE,
∴∠NDM-∠OAN=45°,
而∠OAN=90°-∠ANO=90°-∠DNM,
∴∠NDM-(90°-∠DNM)=45°,
∴∠NDM+∠DNM=135°,
∴180°-∠NMD=135°,
∴∠NMD=45°,
即∠AMD=45°;
(3)①连结OB,如图3,

设F(0,t),
∵△AOF的面积+△BOF的面积=△AOB的面积,
∴![]()
解得:t=![]() ,
,
∴F点坐标为(0,![]() );
);
②存在.
△ABC的面积=![]() ,
,
当P点在y轴上时,设P(0,y),
∵△ABP的三角形=△APF的面积+△BPF的面积,
∴![]() ,
,
解得y=5或y=-2,
∴此时P点坐标为(0,5)或(0,-2);
当P点在x轴上时,设P(x,0),
则![]() ,
,
解得:x=-10或x=4,
∴此时P点坐标为(-10,0),(4,0)
综上所述,满足条件的P点坐标为(0,5);(0,-2);(-10,0),(4,0).


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.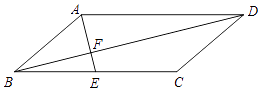
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少? .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠A=90°,AB=AC,∠ABC 的角平分线交 AC 于 D,BD=4 ![]() ,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )
,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )

A.![]() B.2
B.2 ![]() C.3
C.3 ![]() D.2
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com