
【题目】如图所示,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标是
的横坐标是![]() 点
点![]() 的横坐标是
的横坐标是![]() 则以下结论:
则以下结论:
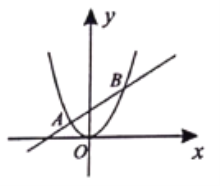
①![]() 时,直线
时,直线![]() 与抛物线
与抛物线![]() 的函数值都随着
的函数值都随着![]() 的增大而增大;②AB的长度可以等于5;③
的增大而增大;②AB的长度可以等于5;③![]() 有可能成为等边三角形;④当
有可能成为等边三角形;④当![]() 时,
时,![]() 时,其中正确的结论是( )
时,其中正确的结论是( )
A.①②B.①③C.①④D.②④
【答案】C
【解析】
①根据图象得到一次函数y=kx+b为增函数,抛物线当x大于0时为增函数,本选项正确;②AB长不可能为5,由A、B的横坐标求出AB为5时,直线AB与x轴平行,即k=0,与已知矛盾;③三角形OAB不可能为等边三角形,因为OA与OB不可能相等;④直线y=-kx+b与y=kx+b关于y轴对称,作出对称后的图象,故y=-kx+b与抛物线交点横坐标分别为-3与2,找出一次函数图象在抛物线上方时x的范围判断即可.
解:①根据图象得:直线y=kx+b(k≠0)为增函数;抛物线y=ax2(a≠0)当x>0时为增函数,则x>0时,直线与抛物线函数值都随着x的增大而增大,本选项正确;
②由A、B横坐标分别为-2,3,若AB=5,可得出直线AB与x轴平行,即k=0,
与已知k≠0矛盾,故AB不可能为5,本选项错误;
③若OA=OB,得到直线AB与x轴平行,即k=0,与已知k≠0矛盾,
∴OA≠OB,即△AOB不可能为等边三角形,本选项错误;
④直线y=-kx+b与y=kx+b关于y轴对称,如图所示:
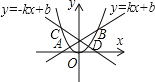
可得出直线y=-kx+b与抛物线交点C、D横坐标分别为-3,2,
由图象可得:当-3<x<2时,ax2<-kx+b,即ax2+kx<b,本选项正确;
则正确的结论有①④.
故选:C.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y ax2 bx c(a≠0)的图象,结论:①abc>0;②a - b c<0;③2a b 0;④ax2bxc2018有两个解,其中正确的个数是( )
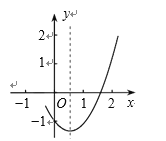
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 图象的顶点在一次函数
图象的顶点在一次函数![]() 的图象上,则称
的图象上,则称![]() 为
为![]() 的伴随函数,如:
的伴随函数,如:![]() 是
是![]() 的伴随函数.
的伴随函数.
(1)若![]() 是
是![]() 的伴随函数,求直线
的伴随函数,求直线![]() 与两坐标轴围成的三角形的面积;
与两坐标轴围成的三角形的面积;
(2)若函数![]() 的伴随函数
的伴随函数![]() 与
与![]() 轴两个交点间的距离为4,求
轴两个交点间的距离为4,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
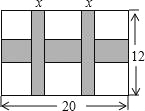
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 与直线
与直线![]() 交于两点
交于两点![]() .已知点
.已知点![]() 坐标为
坐标为![]()
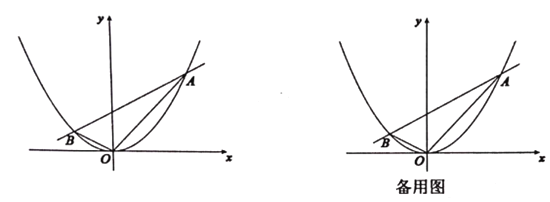
(1)求![]() 点坐标;
点坐标;
(2)求![]() 的面积;
的面积;
(3)将直线![]() 从原点出发向上平移
从原点出发向上平移![]() 个单位,设
个单位,设![]() 为直线平移后其上一点,且满足
为直线平移后其上一点,且满足![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.
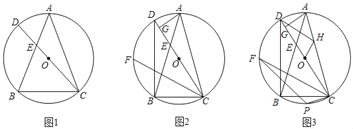
(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中
中![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 与
与![]() 相切于点
相切于点![]() ,在
,在![]() 边上取一点
边上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
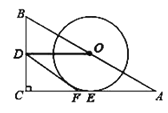
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当![]() ,
,![]() 时,求
时,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
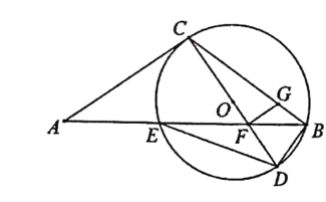
【题目】如图,点E在△ABC的边AB上,过点B,C,E的⊙O切AC于点C.直径CD交BE于点F,连结BD,DE.已知∠A=∠CDE,AC=2![]() ,BD=1.
,BD=1.
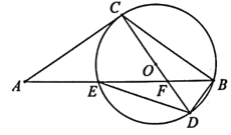
(1)求⊙O的直径.
(2)过点F作FG⊥CD交BC于点G,求FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com