
【题目】小亮和爸爸登山,两人距地面的高度![]() (米)与小亮登山时间
(米)与小亮登山时间![]() (分)之间的函数图象分别如图中折线
(分)之间的函数图象分别如图中折线![]() 和线段
和线段![]() 所示,根据函数图形进行一下探究:
所示,根据函数图形进行一下探究:

(1)设线段![]() 所表示的函数关系式为
所表示的函数关系式为![]() ,根据图象求
,根据图象求![]() 的值,并写出
的值,并写出![]() 的实际意义;
的实际意义;
(2)若小亮提速后,他登山的速度是爸爸速度的3倍,问:小亮登山多长时间时开始提速?此时小亮距地面的高度是多少米?
【答案】(1)![]() ;
;![]()
![]() 表示小亮爸爸的平均登山速度;
表示小亮爸爸的平均登山速度;
![]() 表示小亮爸爸从距地面100米开始登山;
表示小亮爸爸从距地面100米开始登山;
(2)小亮登山2分钟时开始提速,此时小亮距地面的高度为30米.
【解析】
(1)根据图像可知(0,100);(20,300)在线段DE所表示的函数上,从而可解答本题.
(2)分别求出OA段和AC段所对应的函数解析式联立方程组,可求得A点的坐标,从而解答本题.
(1)由图像可知:(0,100);(20,300)在线段DE所表示的函数![]() 上
上
∴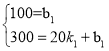 解得
解得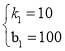
![]() 表示小亮爸爸的平均登山速度;
表示小亮爸爸的平均登山速度;
![]() 表示小亮爸爸从距地面100米开始登山;
表示小亮爸爸从距地面100米开始登山;
(2)由图像可知,点(1,15)在OA段所在的函数图像上,设OA段函数解析式为![]()
∴解得![]() OA段函数解析式为
OA段函数解析式为![]()
点B(m,165)在![]() 上,解得
上,解得![]() ,即点B的坐标为(6.5,165)
,即点B的坐标为(6.5,165)
∵小亮提速后,他登山的速度是爸爸速度的3倍,小亮爸爸的速度为10米/分,点B在AC段上,设AC段的解析式为![]() 可得
可得![]()
∴AC段的函数解析式为![]()
∵点A为OA,AC段的交点
∴![]() 解得
解得![]() 即点A的坐标为(2,30)
即点A的坐标为(2,30)
即小亮登山2分钟时开始提速,此时小亮距地面的高度为30米.


科目:初中数学 来源: 题型:
【题目】某校为贫困山区捐款,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
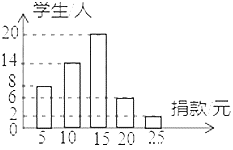
![]() 这50名同学捐款的众数为______元,中位数为______元;
这50名同学捐款的众数为______元,中位数为______元;
![]() 求这50名同学捐款的平均数_______元;
求这50名同学捐款的平均数_______元;
![]() 该校共有1200名学生参与捐款,请估计该校学生的捐款总钱数.
该校共有1200名学生参与捐款,请估计该校学生的捐款总钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
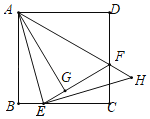
【题目】如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE,△ADF分别沿折痕AE,AF向内折叠,点B,D在点G处重合,过点E作EH⊥AE,交AF的延长线于H,则线段FH的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,我校计划组织师生共![]() 人坐
人坐![]() 、
、![]() 两种型号的大巴车外出春游,且
两种型号的大巴车外出春游,且![]() 型车每辆租金为
型车每辆租金为![]() 元,
元,![]() 型车每辆租金为
型车每辆租金为![]() 元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租
元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人,若租
人,若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人.
人.
(1)请问![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车各有几座?
型大巴车各有几座?
(2)现学校决定租两种型号的大巴车共![]() 辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过
辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过![]() 元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了
元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了![]() 型大巴车
型大巴车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△EFG是两块完全重合的等边三角形纸片,(如图①所示)O是AB(或EF)的中点,△ABC不动,将△EFG绕O点顺时针转α﹝0°<α<120°﹞角.
(1)试分别说明α为多少度时,点F在△ABC外部、BC上、内部(不证明)?
(2)当点F不在BC上时,在图②、图③两种情况下(设EF或延长线与BC交于P,EG与CA或延长线交于Q),分别写出OP与OQ的数量关系,并将图③情况给予说明.
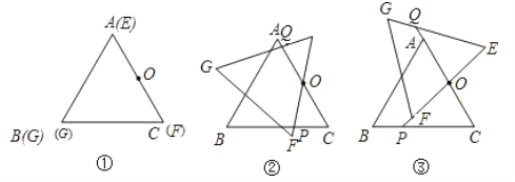
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有![]() 名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
名学生,为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
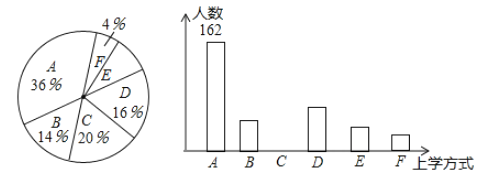
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有_____人,其中选择![]() 类的人数有_____人;
类的人数有_____人;
(2)在扇形统计图中,求![]() 类对应的扇形圆心角
类对应的扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)若将![]() 这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
这四类上学方式视为“绿色出行”,请估计该校选择“绿色出行”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com