
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 4 |
| k |
查看答案和解析>>
科目:初中数学 来源: 题型:
对非负实数x“四舍五入”到个位的值记为![]()
即:当n为非负整数时,如果![]()
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①![]() = (
= (![]() 为圆周率);
为圆周率);
②如果 的取值范围为 ;
的取值范围为 ;
(2)①当![]() ;
;
②举例说明![]() 不恒成立;
不恒成立;
(3)求满足![]() 的值;
的值;
(4)设n为常数,且为正整数,函数![]() 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为![]() 的个数记为b.
的个数记为b.
求证:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:


 = (
= ( 为圆周率);
为圆周率); 的取值范围为 ;
的取值范围为 ; ;
; 不恒成立;
不恒成立; 的值;
的值; 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为 的个数记为b.
的个数记为b.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(河北) 题型:解答题
对非负实数x“四舍五入”到个位的值记为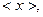
即:当n为非负整数时,如果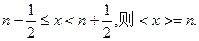
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①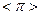 = (
= (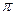 为圆周率);
为圆周率);
②如果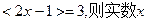 的取值范围为 ;
的取值范围为 ;
(2)①当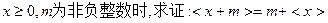 ;
;
②举例说明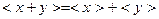 不恒成立;
不恒成立;
(3)求满足 的值;
的值;
(4)设n为常数,且为正整数,函数 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为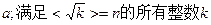 的个数记为b.
的个数记为b.
求证: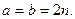
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(河北) 题型:解答题
对非负实数x“四舍五入”到个位的值记为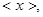
即:当n为非负整数时,如果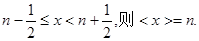
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①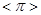 = (
= (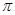 为圆周率);
为圆周率);
②如果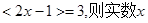 的取值范围为
;
的取值范围为
;
(2)①当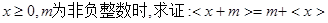 ;
;
②举例说明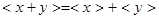 不恒成立;
不恒成立;
(3)求满足 的值;
的值;
(4)设n为常数,且为正整数,函数 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为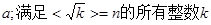 的个数记为b.
的个数记为b.
求证: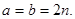
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com