Question

1．如图，在矩形ABCD中，AD=6，CD=4，AD的中点为E，点F是AB边上一点（不与A、B重合），连接EF，把∠A沿EF折叠，使点A落在点G处，连接CG．则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$＜CG＜2$\sqrt{13}$．

Answer 1

分析 分别求得F点在A、B处时的CG的长度即可求得线段CG的取值范围．

解答 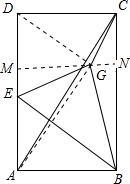解：如图所示，在RT△A，DC中，AD=6，CD=4，
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=2$\sqrt{13}$，
把∠A沿EB折叠，使点A落在点G处，连接AG，DG，
∴∠EAG=∠EGA，AE=EG，
∵AE=DE，
∴EG=ED，
∴∠ADG=∠EGD，
∴∠AGD=∠AGE+∠EGD=∠DAG+∠ADG=90°，
∵AE=3，AB=4，
∴BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=5，
∵$\frac{1}{2}$AG•BE=AE•AB，
∴AG=$\frac{24}{5}$，
在RT△ADG中，DG=$\sqrt{A{D}^{2}-A{G}^{2}}$=$\sqrt{{6}^{2}-（\frac{24}{5}）^{2}}$=$\frac{18}{5}$，
过G点作MN⊥AD，
∴∠AMG=∠AGD=90°，
∵∠MAG=∠GAD，
∴△AMG∽△AGD，
∴$\frac{AM}{AG}$=$\frac{MG}{DG}$=$\frac{AG}{AD}$，即$\frac{AM}{\frac{24}{5}}$=$\frac{MG}{\frac{18}{5}}$=$\frac{\frac{24}{5}}{6}$，
∴AM=$\frac{96}{25}$，MG=$\frac{72}{25}$，
∵BN=AM=$\frac{96}{25}$，MN=CD=4，
∴CN=6-$\frac{96}{25}$=$\frac{54}{25}$，GN=4-$\frac{72}{25}$=$\frac{28}{25}$，
在RT△CNG中，CG=$\sqrt{C{N}^{2}+G{N}^{2}}$=$\frac{2}{5}$$\sqrt{37}$，
∴线段CG的取值范围是 $\frac{2}{5}$$\sqrt{37}$＜CG＜2$\sqrt{13}$，
故答案为$\frac{2}{5}$$\sqrt{37}$＜CG＜2$\sqrt{13}$．

点评 本题考查了翻折的性质，勾股定理的应用，三角形相似的判定和性质，三角形的面积公式的应用等，求得F与A、B重合时CG的长是解题的关键．