练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

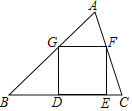
    【题目】如图，已知正方形DEFG的顶点D、E在△ABC的边BC上，顶点G、F分别在边AB、AC上．如果BC=4，△ABC的面积是6，那么这个正方形的边长是_____．

    【答案】

    【解析】作AH⊥BC于H，交GF于M，如图，先利用三角形面积公式计算出AH=3，设正方形DEFG的边长为x，则GF=x，MH=x，AM=3﹣x，再证明△AGF∽△ABC，则根据相似三角形的性质得，然后解关于x的方程即可．

    作AH⊥BC于H，交GF于M，如图，

    ∵△ABC的面积是6，

    ∴BCAH=6，

    ∴AH==3，

    设正方形DEFG的边长为x，则GF=x，MH=x，AM=3﹣x，

    ∵GF∥BC，

    ∴△AGF∽△ABC，

    ∴，即，解得x=，

    即正方形DEFG的边长为，

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

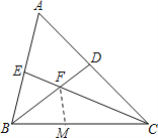
    【题目】在△ABC中，∠A=60°，BD，CE是△ABC的两条角平分线，且BD，CE交于点F，如图所示，用等式表示BE，BC，CD这三条线段之间的数量关系，并证明你的结论；

    晓东通过观察，实验，提出猜想：BE+CD=BC，他发现先在BC上截取BM，使BM=BE，连接FM，再利用三角形全等的判定和性质证明CM=CD即可．

    （1）下面是小东证明该猜想的部分思路，请补充完整；

    ①在BC上截取BM，使BM=BE，连接FM，则可以证明△BEF与______全等，判定它们全等的依据是______；

    ②由∠A=60°，BD，CE是△ABC的两条角平分线，可以得出∠EFB=______°；

    （2）请直接利用①，②已得到的结论，完成证明猜想BE+CD=BC的过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB=AC，AE=AF，连结BF，CE，交于O，连结AO．求证：

    （1）∠B=∠C

    （2）AO平分∠BAC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，E是边CD上一点（点E不与点C、D重合），连结BE．

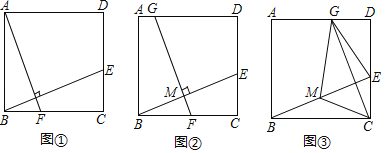
    （感知）如图①，过点A作AF⊥BE交BC于点F．易证△ABF≌△BCE．（不需要证明）

    （探究）如图②，取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．

    （1）求证：BE=FG．

    （2）连结CM，若CM=1，则FG的长为　 　．

    （应用）如图③，取BE的中点M，连结CM．过点C作CG⊥BE交AD于点G，连结EG、MG．若CM=3，则四边形GMCE的面积为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC与△CDE都是等腰直角三角形，∠ACB＝90°，∠DCE＝90°，连结BE，AD，相交于点F．求证：

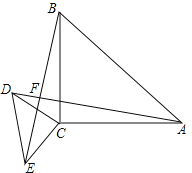
    （1）AD＝BE；

    （2）AD⊥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，正方形ABCD中，P是边BC上一点，BE⊥AP，DF⊥AP，垂足分别是点E、F．

    （1）求证：EF=AE﹣BE；

    （2）联结BF，如课=．求证：EF=EP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知用2辆A型车和1辆B型车载满货物一次可运货物10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．根据以上信息，解答下列问题：

    （1）用1辆A型车和1辆B型车都载满货物一次可分别运货多少吨？

    （2）请你帮该物流公司设计租车方案．若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点若点D为BC边的中点，点M为线段EF上一动点，则周长的最小值为　　

    A. 6 B. 8 C. 10 D. 12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】足球训练中，为了训练球员快速抢断转身，教练在东西方向的足球场上画了一条直线，要求球员在这条直线上进行折返跑训练，如果约定向西为正，向东为负，将某球员的一组折返距练习记录如下(单位：米) ：，．

    球员最后到达的地方在出发点的哪个方向？距出发点多远？

    球员训练过程中，最远处离出发点 米？

    球员在这一组练习过程中，共跑了多少米？

    查看答案和解析>>

    同步练习册答案