
 每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$)
每天早上小明爸爸送他上学,都会看到远处一个巨大的广告牌,小明想知道广告牌离地面有多高,于是特意测量了一下,发现A出观察广告牌底端C的仰角是20°,在B处观察广告牌底端C的仰角是53°,爸爸告诉小明刚才的车速是42千米/时,从A到B用了3秒钟,请你帮小明算一下广告牌底端离地面有多高?(温馨提示:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{4}{3}$,sin20°≈$\frac{3}{10}$,cos20°≈$\frac{9}{10}$,tan20°≈$\frac{2}{5}$) 分析 过点C作CD⊥AB于点D,设CD=x,在直角三角形BDC中易求BD的长,在直角三角形ADC中易求AD的长,再由AB=AD-BD可得关于x的方程,解方程求出x的值即可.
解答 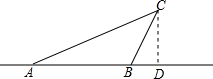 解:过点C作CD⊥AB于点D,设CD=x,
解:过点C作CD⊥AB于点D,设CD=x,
在直角三角形BDC中,
∵∠CBD=53°,CD=x,
∴BD=xtan53°=0.75x,
在直角三角形ADC中,
∵∠CAD=20°,CD=x,
∴AD=2.5x,
∵AB=42×$\frac{3}{3600}$×1000=35米,
∴2.5x-0.75x=35,
解得x=20.
答:广告牌底端离地面有20米高.
点评 本题考查了解直角三角形的应用,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
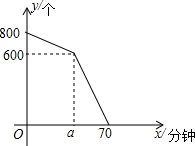 在妇女节前后,某快递总站的快递数量不断增加,每个快递到达总站后都需要进行快递单号的扫描,妇女节当天的早上,快递总站在进行快递单号扫描前,已收到800个未扫描快递,在扫描机开始工作后,仍平均每分钟有10个未扫描快递到达快递总站,扫描机平均每分钟扫描15个快递单号.已知在扫描机开始工作a分钟内只用一台扫描机工作.在妇女节当天未扫描的快递个数y(个)与扫描机工作时间x(分钟)之间的关系如图所示.
在妇女节前后,某快递总站的快递数量不断增加,每个快递到达总站后都需要进行快递单号的扫描,妇女节当天的早上,快递总站在进行快递单号扫描前,已收到800个未扫描快递,在扫描机开始工作后,仍平均每分钟有10个未扫描快递到达快递总站,扫描机平均每分钟扫描15个快递单号.已知在扫描机开始工作a分钟内只用一台扫描机工作.在妇女节当天未扫描的快递个数y(个)与扫描机工作时间x(分钟)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
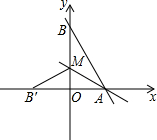 如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则△AMO的面积为9.
如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则△AMO的面积为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
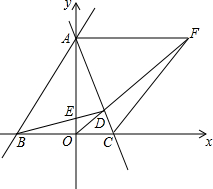 如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.
如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com