

���� ��1���䷽���÷Ǹ��������ʿ����a��b�������A��B���꣬�������������OC�ij��������C�����ꣻ
��2����F��E�ֱ���x�������ߣ�����ֱ�ΪM��N����֤����FMD�ա�END���ɵ�MD=ND�������xE+xF��ֵ��
��3������MA��MC����C��CT��PM��T��֤����CMT�ա�MAH����֤����CGT�ǵ���ֱ�������Σ�����á�CGM=45�㣮
��� �⣺
��1����a2+b2-12a-12b+72=0��
�ࣨa-6��2+��b-6��2=0��
��a=b=6��
��A��6��0����B��0��6����
��OA=6����OC��OA=1��3��
��OC=2��
��C��-2��0����
��2����ͼ2����F��E�ֱ���x�������ߣ�����ֱ�ΪM��N��
�ߵ�BDƽ�֡�BEF�������
��DΪEF�е㣬
��DF=DE��
�ڡ�FMD�͡�END��
$\left\{\begin{array}{l}{��MDF=��NDE}\\{��FMD=��END}\\{DF=DE}\end{array}\right.$
���FMD�ա�END��AAS����
��MD=ND��
��1-xF=xE-1��
��xE+xF=2��
��3�����ı䣬�������£�
��ͼ3������MA��MC����C��CT��PM��T����M��MS��x���ڵ�S��
��M��2��4����C��-2��0����A��6��0����
��S��2��0����
��MS��ֱƽ��AC��
��MC=MA����MS=SC��
���CMA=90�㣬
���CMT+��AMH=��TCM+��CMT=90�㣬
���TCM=��AMH��
�ڡ�CMT�͡�MAH��
$\left\{\begin{array}{l}{��TCM=��AMH}\\{��CTM=��AHM}\\{MC=MA}\end{array}\right.$
���CMT�ա�MAH��AAS����
��TM=AH��CT=MH��
��AH=HG��
��MT=GH��
��GT=GM+MT=MG+GH=MH=CT��
���CGT�ǵ���ֱ�������Σ�
���CGM=45�㣬
������P�ڵ�A�Ҳ��˶�ʱ����CGM�Ķ������ı䣮
���� ������Ҫ����һ�κ������ۺ�Ӧ�ã���Ҫ֪ʶ���е�����ꡢȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ����������ߵ����ʡ���ֱƽ���ߵ����ʵȣ��ڣ�1�����䷽�õ��Ǹ����ĺ�Ϊ0�ǽ���Ĺؼ����ڣ�2����ȷ����DΪEF���е��ǽ���Ĺؼ�������ȫ�������ο��ҵ���E��F������Ĺ�ϵ���ڣ�3���й���������ȫ�ȣ�֤�á�CGTΪ����ֱ���������ǽ���Ĺؼ�������֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
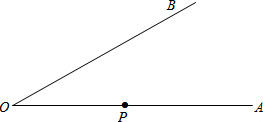 ��ͼ��ʾ����֪��AOB����P��OA�ϣ�
��ͼ��ʾ����֪��AOB����P��OA�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ֱ��y=-x+2�ֱ���x�ᡢy�ύ�ڵ�A��B����PΪ����y=$\frac{\sqrt{2}}{x}$ ��x��0��ͼ���ϵ�һ�㣬����P�ֱ���x�ᡢy��Ĵ��߶�PE��PF����PE��PF�ֱ����߶�AB���ڵ�C��Dʱ����AD•BC��ֵΪ2$\sqrt{2}$��
��ͼ��ʾ��ֱ��y=-x+2�ֱ���x�ᡢy�ύ�ڵ�A��B����PΪ����y=$\frac{\sqrt{2}}{x}$ ��x��0��ͼ���ϵ�һ�㣬����P�ֱ���x�ᡢy��Ĵ��߶�PE��PF����PE��PF�ֱ����߶�AB���ڵ�C��Dʱ����AD•BC��ֵΪ2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����AOE=100�㣬����OD��OB�ǡ�EOC����COA�Ľ�ƽ���ߣ�
��ͼ����AOE=100�㣬����OD��OB�ǡ�EOC����COA�Ľ�ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����֪��ֱ������OABC�У�AB��OC��BC��x���ڵ�C��A��1��1����B��3��1��������P��O���������x����������ÿ��1����λ���ȵ��ٶ��ƶ�����P����PQ��ֱ��ֱ��OA������ΪQ����P���ƶ���ʱ��Ϊt�루0��t��4������OPQ��ֱ������OABC�ص����ֵ����ΪS��
��ͼ��ʾ����֪��ֱ������OABC�У�AB��OC��BC��x���ڵ�C��A��1��1����B��3��1��������P��O���������x����������ÿ��1����λ���ȵ��ٶ��ƶ�����P����PQ��ֱ��ֱ��OA������ΪQ����P���ƶ���ʱ��Ϊt�루0��t��4������OPQ��ֱ������OABC�ص����ֵ����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��B��C�����ǵ�����ABC���������㣬��ƽ��ֱ������ϵ�е�����ΪB��0��3����C��4��0��������������A������ϵ��x���ϣ����A�����꣮
��ͼ��B��C�����ǵ�����ABC���������㣬��ƽ��ֱ������ϵ�е�����ΪB��0��3����C��4��0��������������A������ϵ��x���ϣ����A�����꣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com