
分析 由已知得出∠A=90°,BC=OA=4,OB=AC=7,分两种情况:(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,当A'E:A'F=1:3时,求出A'E=1,A'F=3,由折叠的性质得:OA'=OA=4,∠OA'D=∠A=90°,在Rt△OA'F中,由勾股定理求出OF=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,即可得出答案;
②当A'E:A'F=3:1时,同理得:A'($\sqrt{15}$,1);
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,由A'F:A'E=1:3,则A'F:EF=1:2,求出A'F=$\frac{1}{2}$EF=$\frac{1}{2}$BC=2,在Rt△OA'F中,由勾股定理求出OF=2$\sqrt{3}$,即可得出答案.
解答 解: ∵点A(0,4),B(7,0),C(7,4),
∵点A(0,4),B(7,0),C(7,4),
∴BC=OA=4,OB=AC=7,
分两种情况:
(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,如图1所示:
①当A'E:A'F=1:3时,
∵A'E+A'F=BC=4,
∴A'E=1,A'F=3,
由折叠的性质得:OA'=OA=4,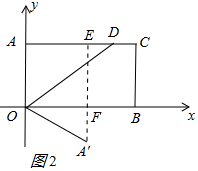
在Rt△OA'F中,由勾股定理得:OF=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴A'($\sqrt{7}$,3);
②当A'E:A'F=3:1时,同理得:A'($\sqrt{15}$,1);
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,如图2所示:∵A'F:A'E=1:3,则A'F:EF=1:2,
∴A'F=$\frac{1}{2}$EF=$\frac{1}{2}$BC=2,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴A'(2$\sqrt{3}$,-2);
故答案为:($\sqrt{7}$,3)或($\sqrt{15}$,1)或(2$\sqrt{3}$,-2).
点评 本题考查了折叠的性质、矩形的性质、坐标与图形性质、勾股定理等知识;熟练掌握折叠的性质和勾股定理是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 方程2x-1=x+5移项,得2x+x=5+1 | |
| B. | 方程$\frac{x}{2}$+$\frac{x}{3}$=1去分母,得3x+2x=1 | |
| C. | 方程-7x=4系数化为1,得x=-$\frac{7}{4}$ | |
| D. | 方程(x+2)-2(x-1)=0去括号,得x+2-2x+2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件A和B都是随机事件 | B. | 只有事件B是随机事件 | ||
| C. | 只有事件A是随机事件 | D. | 事件A和B都不是随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | -8 | C. | $\frac{1}{16}$ | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
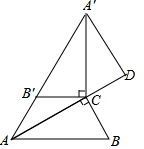 如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )
如图,△ABC中,∠ACB=90°,∠B=60°,BC=$\sqrt{3}$,△A′B′C由△ABC绕C点顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,恰好A,B′,A′在同一条直线上,A′D∥BC交AC的延长线于点D,则A′D的长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
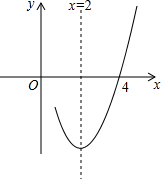 已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:| A. | ①②③ | B. | ③④⑤ | C. | ①②④ | D. | ①④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2+1 | B. | y=(x+2)2-1 | C. | y=(x-2)2+1 | D. | y=(x-2)2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com