练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，C、D是线段AB的三等分点，且AD=4，求AB的长．

    6

    解析试题分析：根据已知得出AC=CD=BD，求出BD，代入AD+BD求出即可．
    试题解析：C、D是线段AB的三等分点，AD=4，
    ∵AC=CD=BD=AD=2，
    ∴AB=AD+BD=4+2=6，
    即AB的长是6．
    考点：两点间的距离．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数．请将解题过程填写完整．
    解：∵EF∥AD（已知）
    ∴∠2=　_________　（　　）
    又∵∠1=∠2（已知）
    ∴∠1=∠3（　　）
    ∴AB∥　_________　（　　）
    ∴∠BAC+　_________　=180°（　　）
    ∵∠BAC=70°（已知）
    ∴∠AGD=　_________　．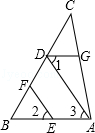

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．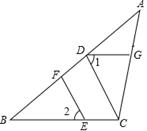

    （1）CD与EF平行吗？为什么？
    （2）如果∠1=∠2，那么DG∥BC吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，，是线段的三等分点，D是线段CB上一点，CD比DB长4cm，求AD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，点C在线段AB上，AC＝8cm，CB＝6cm，点M、N分别是AC、BC的中点．

    （1）求线段MN的长；
    （2）若C为线段AB上任一点，满足AC＋CB＝a cm，其它条件不变，你能猜想MN的长度吗？并说明理由；
    （3）若C在线段AB的延长线上，且满足AC－CB＝b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知DE∥BC，CD是∠ACB的平分线，∠B＝70°，∠ACB＝50°，求∠EDC和∠BDC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，AD∥BC，BD平分∠ABC．求证：AB=AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    推理填空：
    如图，已知∠1 =∠2，∠B =∠C，可推得AB∥CD。理由如下：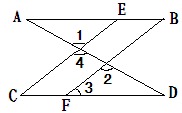

    ∵ ∠1 =∠2（已知），且∠1 =∠4（                   ），
    ∴ ∠2 =∠4（等量代换），
    ∴  CE∥BF（                                    ）.
    ∴ ∠    =∠3（                               ）.
    又∵ ∠B =∠C（已知），
    ∴ ∠3 =∠B（等量代换），
    ∴  AB∥CD（                                    ）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，铁路道口的栏杆短臂长1m，长臂长16m．当短臂端点下降0.5m时，长臂端点升高（杆的宽度忽略不计）（   ）

    A．4m B．6m C．8m D．12m

    查看答案和解析>>

    同步练习册答案