
 小明做了一个如图所示的“风筝”骨架,其中AB=AD,CB=CD.
小明做了一个如图所示的“风筝”骨架,其中AB=AD,CB=CD.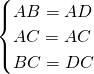
 ×BD×AE+
×BD×AE+ ×BD×CE
×BD×CE ×BD×(AE+CE)
×BD×(AE+CE) BD×AC
BD×AC ab.
ab. BD×AC,代入求出即可.
BD×AC,代入求出即可.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 14、小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH平分∠EDF,即∠EDH=∠FDH.小明说得对吗?试说明理由.
14、小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH平分∠EDF,即∠EDH=∠FDH.小明说得对吗?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 14、小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是
14、小明做了一个如图所示的风筝,其中EH=FH,ED=FD,小明说不用测量就知道DH是EF的垂直平分线.其中蕴含的道理是查看答案和解析>>
科目:初中数学 来源: 题型:
 小明做了一个如图所示的“风筝”骨架,其中AB=AD,CB=CD.
小明做了一个如图所示的“风筝”骨架,其中AB=AD,CB=CD.查看答案和解析>>
科目:初中数学 来源: 题型:
 小明做了一个如图所示的风筝(如图1),他想验证∠ABC与∠ADC是否相等(如图2),但手头只有一把足够长的尺子,你能帮他像个办法吗?并说明你这样做的理由.
小明做了一个如图所示的风筝(如图1),他想验证∠ABC与∠ADC是否相等(如图2),但手头只有一把足够长的尺子,你能帮他像个办法吗?并说明你这样做的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com