
 如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).
如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4). 分析 (1)正确,先证明△ABD为等边三角形,根据“SAS”证明△AED≌△DFB;
(2)错误,只要证明△GDC≌△BGC,利用等腰三角形性质即可解决问题.
(3))正确,由△AED≌△DFB,推出∠ADE=∠DBF,所以∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,
(4)正确,证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG=S四边形CMGN,易求后者的面积.
解答 解:(1)∵四边形ABCD为菱形,
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
在△AED和△DFB中,
$\left\{\begin{array}{l}{AE=DF}\\{∠A=∠BDF}\\{AD=BD}\end{array}\right.$,
∴△AED≌△DFB,故本小题正确; (2)当点E,F分别是AB,AD中点时(如图1),
(2)当点E,F分别是AB,AD中点时(如图1),
由(1)知,△ABD,△BDC为等边三角形,
∵点E,F分别是AB,AD中点,
∴∠BDE=∠DBG=30°,
∴DG=BG,
在△GDC与△BGC中,
$\left\{\begin{array}{l}{DG=BG}\\{CG=CG}\\{CD=CB}\end{array}\right.$,
∴△GDC≌△BGC,
∴∠DCG=∠BCG,
∴CH⊥BD,即CG⊥BD,故本选项错误;
(3)∵△AED≌△DFB,
∴∠ADE=∠DBF,
∴∠BGE=∠BDG+∠DBG=∠BDG+∠ADE=60°,故本选项正确.
(4)∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.(如图2)
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN,
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=$\frac{1}{2}$CG,CM=$\frac{\sqrt{3}}{2}$CG,
∴S四边形CMGN=2S△CMG=2×$\frac{1}{2}$×$\frac{1}{2}$CG×$\frac{\sqrt{3}}{2}$CG=$\frac{\sqrt{3}}{4}$CG2,故本小题正确.
综上所述,正确的结论有(1)(3)(4).
故答案为:((1)(3)(4).
点评 此题综合考查了菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,作出辅助线构造出全等三角形,把不规则图形的面转化为两个全等三角形的面积是解题的关键.


科目:初中数学 来源: 题型:选择题
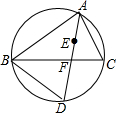 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )| A. | $\frac{3}{2}$∠D-90° | B. | 90°-$\frac{1}{2}$∠D | C. | 180°-∠D | D. | 3∠D-180° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为$\sqrt{3}$-1.
如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为$\sqrt{3}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=4,BC=6,点E为BC的中点,连接AE,将△ABE沿AE折叠,点B落在点B′处,则sin∠B′EC的值为$\frac{24}{25}$.
如图,矩形ABCD中,AB=4,BC=6,点E为BC的中点,连接AE,将△ABE沿AE折叠,点B落在点B′处,则sin∠B′EC的值为$\frac{24}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:
如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )
如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com