
【题目】问题提出
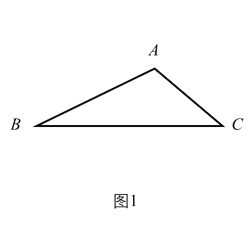
(1)如图(1),已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,求点
,求点![]() 到
到![]() 的最短距离.
的最短距离.
问题探究
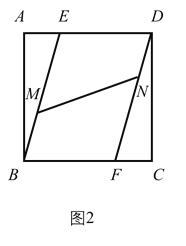
(2)如图(2),已知边长为3的正方形![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 和
和![]() 上,且
上,且![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,若点
,若点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的动点,连接
上的动点,连接![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
问题解决
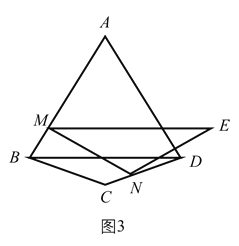
(3)如图(3),已知在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,将线段
,将线段![]() 沿方向
沿方向![]() 平移至
平移至![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 为边
为边![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,
,![]() 的长度是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
的长度是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
【答案】(1)2;(2)![]() ;(3)
;(3)![]()
【解析】
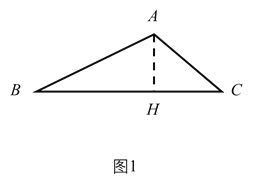
(1)如图1中,作AH⊥BC于H.设AH=CH=x,根据![]() ,构建方程即可解决问题.
,构建方程即可解决问题.
(2)如图2中,作EJ⊥DF于J.利用相似三角形的性质求出EJ,再根据垂线段最短即可解决问题.
(3)如图3中,如图3中,记MN的中垂线与AC的交点为点O,连接OM,ON,OB,OD,并以点O为圆心,OM为半径长作⊙O.以点O为圆心,OM为半径作圆,当⊙O与CD相切于 N时,即此时⊙O也与AB,BC相切,切点分别为M,G,此时MN最小.连接OG.设AC交BD于J,作AT⊥BC于T.利用相似三角形的性质求出MN即可.
解:(1)如图1中,作AH⊥BC于H.
在Rt△ACH中,∵∠C=45°,∠AHC=90°,
∴AH=CH,设AH=CH=x.
在Rt△ABH中,∵∠AHB=90°,∠B=30°,
∴BH=![]() ,
,
∴![]()
∴x=2,即AH=2,
∴点A到BC的最短距离为2.
(2)如图2中,作EJ⊥DF于J,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=3,
∵![]() ,
,![]() ,
,
∴AE=CF=1,DE=BF=2,
∴DF=![]() ,
,
∵DE∥BF,
∴四边形BEDF是平行四边形,
∴BE∥DF,
∵EJ⊥DF,
∴∠EJD=∠EDC=∠C=90°,
∴∠EDJ+∠CDF=90°,∠CDF+∠CFD=90°,
∴∠EDJ=∠CFD,
∴△EDJ∽△DFC,
∴![]() ,
,
即![]()
∴![]() ,
,
根据垂线段最短可知,MN的最小值为=![]() ;
;
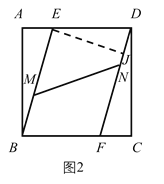
(3)如图3中,记MN的中垂线与AC的交点为点O,连接OM,ON,OB,OD,并以点O为圆心,OM为半径长作⊙O.以点O为圆心,OM为半径作圆,当⊙O与CD相切于 N时,即此时⊙O也与AB,BC相切,切点分别为M,G,此时MN最小.连接OG.设AC交BD于J,作AT⊥BC于T.
在Rt△ABT中,∵∠ATB=90°,AB=3,∠ABT=60°,
∴BT=![]() ,AT=
,AT=![]() ,
,
∴CT=BCBT=![]() ,
,
∴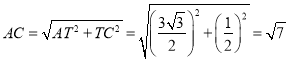 ,
,
∵AB=AD,CB=CD,
∴AC⊥BD,BJ=DJ,
∴![]()
∴![]() ,
,
∵OM=OG,OM⊥AB,OG⊥BC,
∴OB平分∠ABC,
∴∠OBM=![]() ,
,
∴OB=2OM,
∵OB=OD,OM=ON,BM=DN,
∴△OMB≌△OND(SSS),
∴∠BOM=∠NOD,
∴∠MON=∠BOD,
∵OM=ON,OB=OD,
∴△MON∽△BOD,
∴![]() ,
,
∴![]() ,
,
∴MN的最小值为:![]() .
.


科目:初中数学 来源: 题型:
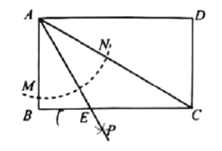
【题目】如图,矩形![]() 以点
以点![]() 为圆心,以任意长为半径作弧分别交
为圆心,以任意长为半径作弧分别交![]() 、
、![]() 于
于![]() 两点,再分别以点
两点,再分别以点![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧交于点
的长为半径作弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则矩形
,则矩形![]() 的面积等于__________.
的面积等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
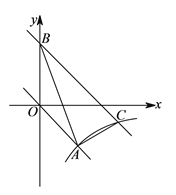
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩(单位:分),根据成绩分成如下四个组:![]() ,
,![]() ,
,![]() ,
,![]() ,并制作出如下的扇形统计图和频数分布直方图.
,并制作出如下的扇形统计图和频数分布直方图.
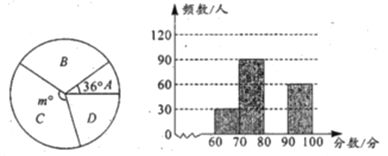
请根据图表中的信息,解答下列问题:
(1)扇形统计图中的![]() ________,并补全频数分布直方图.
________,并补全频数分布直方图.
(2)4个小组每组推选1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或面树状图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校数学社团成员想利用所学的知识测量某广告牌的宽度(图中线段MN的长).直线MN垂直于地面,垂足为点P,在地面A处测得点M的仰角为60°,点N的仰角为45°,在B处测得点M的仰角为30°,AB=5米.且A、B、P三点在一直线上,请根据以上数据求广告牌的宽MN的长.(结果保留根号)
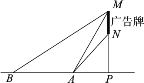
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年4月23日是我国第一个“全民阅读日”某校开展了“建设书香校园,捐赠有益图书”活动.我们在参加活动的所有班级中,随机抽取了一个班,已知这个班是八年级5班,全班共50名学生.现将该班捐赠图书情况的统计结果,绘制成如下两幅不完整的统计图.
请你根据以上信息,解答下列问题:
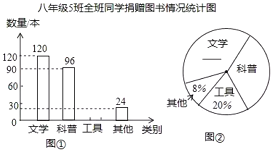
(1)补全上面的条形统计图和扇形统计图;
(2)求八年级5班平均每人捐赠了多少本书?
(3)若该校八年级共有800名学生,请你估算这个年级学生共可捐赠多少本书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点和抛物线与
的顶点和抛物线与![]() 轴的交点在一次函数
轴的交点在一次函数![]() 的图象上,它的对称轴是
的图象上,它的对称轴是![]() ,有下列四个结论:①
,有下列四个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
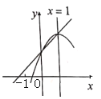
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠D=30°,AB<AD.
(1)在AD边上求作一点P,使点P到边AB,BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接BP,若AB=2,求△ABP的面积.
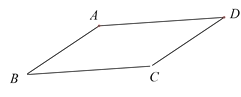
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列正多边形都满足BA1=CB1,在正三角形中,我们可推得:∠AOB1=60°;在正方形中,可推得:∠AOB1=90°;在正五边形中,可推得:∠AOB1=108°,依此类推在正八边形中,AOB1=____°,在正n(n≥3)边形中,∠AOB1=____°.
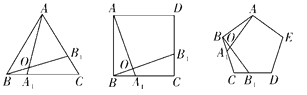
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com