
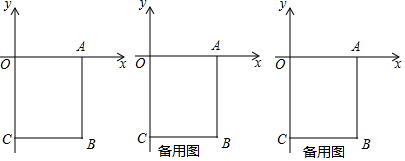
���� ��1������a��c�����ϵʽa=$\frac{\sqrt{{c}^{2}-64}+\sqrt{64{-c}^{2}}}{c-8}$+6���ɵ�$\left\{\begin{array}{l}{{c}^{2}-64��0}\\{64-{c}^{2}��0}\\{c��8}\end{array}\right.$�����c=-8��a=6���ɴ˼��ɽ�����⣮
��2�����������ηֱ����ٵ�0��t��8ʱ���ڵ�8��t��14ʱ��
��3�����ۣ���PEA+��PFC=150����PFC-��AEP=30�㣮���������ηֱ�����ͼ�ν���֤�����ɣ�
��� �⣺��1����a��c�����ϵʽa=$\frac{\sqrt{{c}^{2}-64}+\sqrt{64{-c}^{2}}}{c-8}$+6��
��$\left\{\begin{array}{l}{{c}^{2}-64��0}\\{64-{c}^{2}��0}\\{c��8}\end{array}\right.$��
��c=-8��a=6��
��A��6��0����B��6��-8����C��0��-8����
��2����ͼ1�У��ٵ�0��t��8ʱ��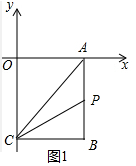
S=$\frac{1}{2}$•AB•CB=$\frac{1}{2}$•t•6=3t��
�ڵ�8��t��14ʱ��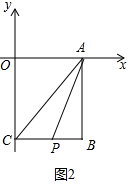
S=$\frac{1}{2}$•PC•AB=$\frac{1}{2}$•��14-t��•8=-4t+56��
����������S=$\left\{\begin{array}{l}{3t}&{��0��t��8��}\\{-4t+56}&{��8��t��14��}\end{array}\right.$��
��3���ٵ���P���߶�AB��ʱ��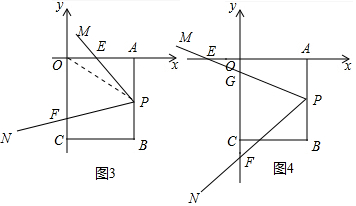
��ͼ3�У����ۣ���PEA+��PFC=150�㣮
���ɣ�����OP��
�ߡ�PFC=��FPO+��FOP����AEP=��EOP+��EPO��
���PEA+��PFC=��FPO+��FOP+��EOP+��EPO=��AOF+��EPF=90��+60��=150�㣮
��ͼ4�У����ۣ���PFC-��AEP=30�㣬
���ɣ�ʱPM��OC��G��
�ߡ�AEP+��EGO=90�㣬��EGO=��PGF=120��-��PFC��
���AEP+120��-��PFC=90�㣬
���PFC-��AEP=30�㣬
�ڵ���P���߶�BC��ʱ��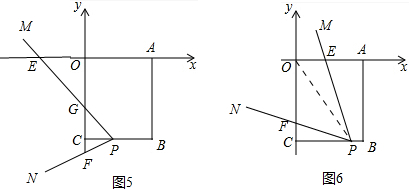
��ͼ5�У����ۣ���PFC-��AEP=30�㣬
���ɣ�ʱPM��OC��G��
�ߡ�AEP+��EGO=90�㣬��EGO=��PGF=120��-��PFC��
���AEP+120��-��PFC=90�㣬
���PFC-��AEP=30�㣮
��ͼ6�У����ۣ���PEA+��PFC=150�㣮
���ɣ�����OP��
�ߡ�PFC=��FPO+��FOP����AEP=��EOP+��EPO��
���PEA+��PFC=��FPO+��FOP+��EOP+��EPO=��AOF+��EPF=90��+60��=150�㣮
������������PEA+��PFC=150����PFC-��AEP=30�㣮
���� ���⿼���������ۺ��⡢���ε����ʡ����θ�ʽ�����ʡ������ε������֪ʶ������Ĺؼ���ѧ���÷������۵�˼��˼�����⣬�����п��������ͣ�


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 0 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
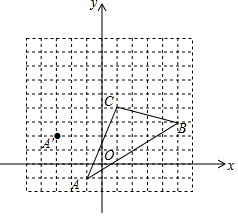 ��ͼ����ABC�����������ֱ�ΪA��-1��-1����B��5��3����C��1��4����
��ͼ����ABC�����������ֱ�ΪA��-1��-1����B��5��3����C��1��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
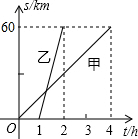 A��B�������60km���������˷ֱ������г���Ħ�г�����ͬ·��������ʻ����A�ص���B�أ�������ʻ��·��s��km����׳������ʱ��t��h��֮��ĺ���ͼ����ͼ��ʾ
A��B�������60km���������˷ֱ������г���Ħ�г�����ͬ·��������ʻ����A�ص���B�أ�������ʻ��·��s��km����׳������ʱ��t��h��֮��ĺ���ͼ����ͼ��ʾ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
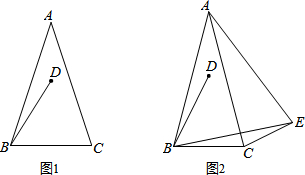
 ��ͼ��ֱ��l1��l2��l3����l1��l2�ľ���Ϊ1��l2��l3�ľ���Ϊ2��������ABC�Ķ���ֱ���ֱ��l1��l2��l3�ϣ�AB=AC����BAC=120�㣬����������ε�����Ϊ2��$\frac{2\sqrt{39}}{3}$��$\frac{2\sqrt{57}}{3}$��
��ͼ��ֱ��l1��l2��l3����l1��l2�ľ���Ϊ1��l2��l3�ľ���Ϊ2��������ABC�Ķ���ֱ���ֱ��l1��l2��l3�ϣ�AB=AC����BAC=120�㣬����������ε�����Ϊ2��$\frac{2\sqrt{39}}{3}$��$\frac{2\sqrt{57}}{3}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com