练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，将△ABC绕点C按顺时针方向旋转至△A′B′C，使点A′落在BC的延长线上．已知∠A=27°，∠B=40°，则∠ACB′是（　　）
    A．46°B．45°C．44°D．43°

    分析 先利用三角形外角性质得∠ACA′=∠A+∠B=67°，再根据旋转的性质得∠BCB′=∠ACA′=67°，然后利用平角的定义计算∠ACB′的度数．

    解答 解：∵∠A=27°，∠B=40°，
    ∴∠ACA′=∠A+∠B=67°，
    ∵△ABC绕点C按顺时针方向旋转至△A′B′C，
    ∴∠BCB′=∠ACA′=67°，
    ∴∠ACB′=180°-67°-67°=46°．
    故选A．

    点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．已知x、y为实数，且（x2+y2）（x2+y2+1）=20．求x2+y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知关于x的一元二次方程x2-2x+m-1=0．
    （1）若方程有实数根，求实数m的取值范围；
    （2）若方程两实数根为x1，x2，且满足4x1+3x2=7，求实数m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．为了更好保护水资源，造福人类．某工厂计划建一个容积V（m3）一定的圆柱状污水处理池，池的底面积S（m2）关于深度h（m）的函数图象大致是（　　）
    A．B．C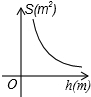．D．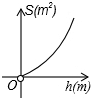

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．化简：$（{\frac{2}{x+2}-\frac{2}{x-2}}）÷\frac{4}{{{x^2}-4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

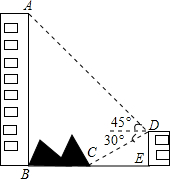    12．如图，大楼沿右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同-水平直线上．己知AB=80m，DE=10m，求障碍物B、C两点间的距离（结果精确到0.1m）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：${（\sqrt{2}-1）}^{-1}$+$\sqrt{8}$-6sin45°+（-1）2009．

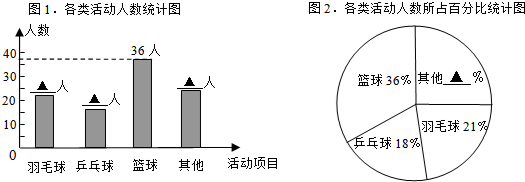
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，⊙O过△ABC的顶点A、B、C，且∠C=30°，AB=3，则弧AB长为π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．学校为统筹安排大课间体育活动，在各班随机选取了一部分学生，分成四类活动：“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查，整理收集到的数据，绘制成如下的两幅统计图．

    （1）学校采用的调查方式是抽样调查；学校共选取了100名学生；
    （2）补全统计图中的数据：条形统计图中羽毛球21人、乒乓球18人、其他25人、扇形统计图中其他25%；
    （3）该校共有1200名学生，请估计喜欢“乒乓球”的学生人数．

    查看答案和解析>>

    同步练习册答案