
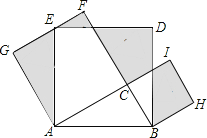
【题目】如图,![]() 中,
中,![]() 分别以
分别以![]() 为边在
为边在![]() 的同侧作正方形
的同侧作正方形![]() ,则图中阴影部分的面积之和为_______.
,则图中阴影部分的面积之和为_______.
【答案】![]()
【解析】
过D作BF的垂线交BF于N,连接DI,通过证明S1+S2+S3+S4=Rt△ABC的面积×3,依此即可求解.
解:过D作BF的垂线交BF于N,连接DI,
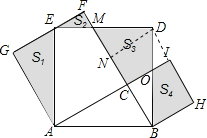
∵四边形![]() 、四边形
、四边形![]() 和四边形
和四边形![]() 为正方形,
为正方形,
∴GA=AC=GF,∠G=∠ABD=90°,AE=AB=BD,BC=CI,∠H=∠ICB=90°,
∵DN⊥BF,
∴∠DNB=90°,∠NDB+∠NBD=90°,
又∵∠ABD=∠NBA+∠NBD=90°,
∴∠NBA=∠NDB,
在△ACB和△BND中
∵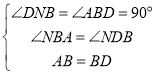
∴△ACB≌△BND(AAS),
∴BC=DN=IC,BN=AC,
又∵∠DNB=∠ICB=90°,
∴DN∥CI,
∴四边形DNCI是平行四边形,且平行四边形DNCI是矩形,
∴∠DIC=90°,
∴D、I、H三点共线,
∵∠ACB=90°,
∴∠G=∠ACB=90°,
在![]() 和
和![]() 中
中
∵![]()
∴![]() ≌
≌![]() (HL)
(HL)
∴GE=BC,
同理可证![]() ≌
≌![]() ,
,
∵∠BDE=∠ICB=90°,
∴∠DBM+∠DMB=90°,∠DBM+∠AOB=90°,
∴∠DMB=∠AOB,
∴∠EMF=∠DOI,
在△MND和△BCO中,
∵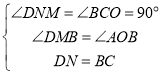
∴△MND≌△BCO,
∵DI=BN-BC,EF=GF-GE,
∴EF=DI,
在△EFM和△DIO中
∵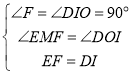
∴△EFM≌△DIO,
∵![]()
∴![]() ,
,
∴Rt△ABC的面积=![]() ,
,
∴S1+S2+S3+S4
=S1+S3+(S2+S4),
=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
=Rt△ABC的面积×3=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.

(1)该顾客最少可得_________元购物券,最多可得_________元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和
和![]() .
.
(1)在同一直角坐标系内,画出这两个函数的大致图象;

(2)直接写出:①函数![]() 与坐标轴围成的图形的面积为_______;
与坐标轴围成的图形的面积为_______;
②函数![]() 与坐标轴围成的图形的面积为________;
与坐标轴围成的图形的面积为________;
③这两个函数图象与![]() 轴围成的图形的面积为_________.
轴围成的图形的面积为_________.
(3)若反比例函数![]() 经过这两个函数图象的交点,则k的值为______.
经过这两个函数图象的交点,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
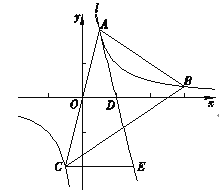
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分14分)在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
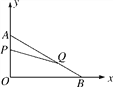
(1)求直线AB的解析式;
(2)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时,四边形OPQB的面积为多少个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 是
是![]() 上任一点,
上任一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() 是等腰三角形;②
是等腰三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论是( )
,其中正确的结论是( )

A.①②B.①③④C.①④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com