

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源:2005年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
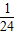 x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-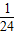 x2+6始终有公共点,请在图一中作出这样的公共点.
x2+6始终有公共点,请在图一中作出这样的公共点.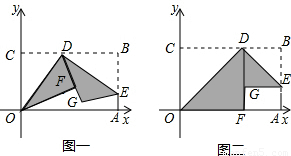
查看答案和解析>>
科目:初中数学 来源:2005年江苏省苏州市中考数学试卷(解析版) 题型:解答题
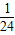 x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-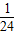 x2+6始终有公共点,请在图一中作出这样的公共点.
x2+6始终有公共点,请在图一中作出这样的公共点.
查看答案和解析>>
科目:初中数学 来源:2005年江苏省苏州市中考数学试卷(解析版) 题型:选择题
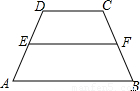
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com