
分析 (1)设两根分别为2k,3k,列出方程组,消去k即可证明.
(2)求出$\frac{{b}^{2}}{{a}^{2}}$=25k2,$\frac{{c}^{2}}{{a}^{2}}$=900k4,得$\frac{{c}^{2}}{{a}^{2}}$-$\frac{{b}^{2}}{{a}^{2}}$=900k4-25k2,由c2-b2=a2,列出方程即可解决问题.
解答 (1)证明:∵两根之比为2:3,设两根分别为2k,3k,则有$\left\{\begin{array}{l}{2k+3k=-\frac{b}{a}}\\{2k•3k=\frac{c}{5a}}\end{array}\right.$,
由①得到k=-$\frac{b}{5a}$代入②得到6(-$\frac{b}{5a}$)2=5ac,
∴6b2=5ac.
(2)∵5k=-$\frac{b}{a}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=25k2,
∵6k2=$\frac{c}{5a}$,
∴$\frac{{c}^{2}}{{a}^{2}}$=900k4,
∴$\frac{{c}^{2}}{{a}^{2}}$-$\frac{{b}^{2}}{{a}^{2}}$=900k4-25k2,
∵c2-b2=a2,
∴900k4-25k2-1=0,
∴(45k2+1)(20k2-1)=0,
∴k2=$\frac{1}{20}$,
∵k>0,
∴k=$\frac{\sqrt{5}}{10}$,
∴f方程的两根为$\frac{\sqrt{5}}{5}$和$\frac{3\sqrt{5}}{10}$.
点评 本题考查根与系数关系,解题的关键是记住x1+x2=$\frac{b}{a}$,x1x2=$\frac{c}{a}$,学会用方程的思想思想思考问题,属于中考常考题型.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A、B、C、D在⊙O上,AC、BD相交于点P.则图中相似三角形有2对;若点C是$\widehat{BD}$的中点,则图中相似三角形有4对.
如图,点A、B、C、D在⊙O上,AC、BD相交于点P.则图中相似三角形有2对;若点C是$\widehat{BD}$的中点,则图中相似三角形有4对.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
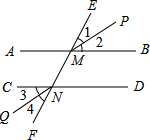 如图,下面四个条件中,请你以其中两个为已知条件,第三个作为结论,推出一个正确的命题.(只需写出一种情况)①AB∥CD;②∠1=∠4;③∠3=∠2;④MP∥NQ.
如图,下面四个条件中,请你以其中两个为已知条件,第三个作为结论,推出一个正确的命题.(只需写出一种情况)①AB∥CD;②∠1=∠4;③∠3=∠2;④MP∥NQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com