
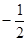 x2+bx+c过点(-6,-2),与y轴交于点C,且对称轴与x轴交于点B(-2,0),顶点为A.
x2+bx+c过点(-6,-2),与y轴交于点C,且对称轴与x轴交于点B(-2,0),顶点为A.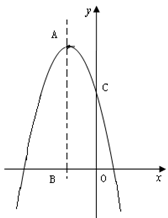
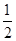 x+2.
x+2.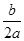 =﹣2,
=﹣2,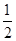 x2﹣2x+c,
x2﹣2x+c,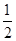 x2+bx+c过点(﹣6,﹣2),
x2+bx+c过点(﹣6,﹣2),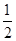 ×(﹣6)2﹣2×(﹣6)+c,解得c=4,
×(﹣6)2﹣2×(﹣6)+c,解得c=4,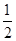 x2﹣2x+4,
x2﹣2x+4,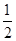 x2﹣2x+4=﹣
x2﹣2x+4=﹣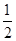 (x2+4x+4)+6)=﹣
(x2+4x+4)+6)=﹣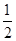 (x+2)2+6
(x+2)2+6
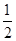 x2﹣2x+4,(﹣2,2)合适,(﹣6,2)不合适,
x2﹣2x+4,(﹣2,2)合适,(﹣6,2)不合适,
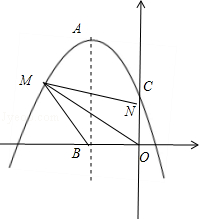
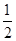 x+2;
x+2;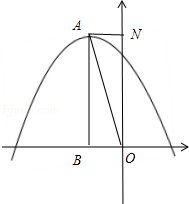
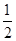 x+2.
x+2.

 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:不详 题型:解答题
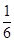 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
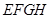 与
与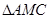 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;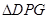 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
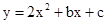 的图象经过(
的图象经过(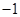 ,0)和(
,0)和(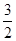 ,0)两点.
,0)两点.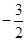 <x<1时,y的取值范围.
<x<1时,y的取值范围.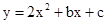 图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点 .
. 、
、 的坐标分别是
的坐标分别是 ( ),
( ), ( );
( ); 上且经过点
上且经过点 的抛物线的解析式;
的抛物线的解析式; 向上平移,平移后的抛物线交
向上平移,平移后的抛物线交 轴于点
轴于点 ,顶点为点
,顶点为点 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1)。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com