
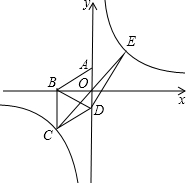
 如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.
如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.分析 (1)只要求出点C坐标即可解决问题.
(2)如图1中,作DF⊥BC于F,连接PB,PD,PF,设P(a,$\frac{2\sqrt{3}}{a}$),由S△BDP=2S△CDE,得S△PBF+S△PDF-S△BDF=4S△COD,列出方程即可解决问题.
(3)存在.分三种情形讨论①如图2中,当OK=KH时,设OK=KH=b,作HF⊥OB于F.②如图3中,当OK=OH时,设OK=OH=b,③如图4中,当OK=KH时,设OK=KH=b,作OF⊥AB于F.分别列出方程解决问题即可.
解答 解:(1)∵A(0,1),B(-$\sqrt{3}$,0),
∵OA=1,OB=$\sqrt{3}$,
在Rt△AOB中,AB=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵四边形ABCD是菱形,
∴AB=BC=AD=CD=2,
∴C(-$\sqrt{3}$,-2),D(0,-1),
∵双曲线y=$\frac{m}{x}$经过点C,
∴m=2$\sqrt{3}$,
∴反比例函数的解析式为y=$\frac{2\sqrt{3}}{x}$.
(2)如图1中,作DF⊥BC于F,连接PB,PD,PF,设P(a,$\frac{2\sqrt{3}}{a}$),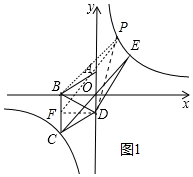
∵S△BDP=2S△CDE,
∴S△PBF+S△PDF-S△BDF=4S△COD,
∴$\frac{1}{2}$×1×(a+$\sqrt{3}$)+$\frac{1}{2}$×$\sqrt{3}$×(1+$\frac{2\sqrt{3}}{a}$)-$\frac{1}{2}$×1×$\sqrt{3}$=4×$\frac{1}{2}$×1×$\sqrt{3}$,
∴a=$\sqrt{3}$或2$\sqrt{3}$,
∴P($\sqrt{3}$,2)或(2$\sqrt{3}$,1).
(3)存在.
①如图2中,当OK=KH时,设OK=KH=b,作HF⊥OB于F.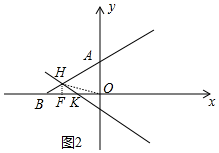
∵∠HBK=∠HKF=30°,
∴HB=HK,BF=FK=$\frac{\sqrt{3}}{2}$b,
∴$\sqrt{3}$b+b=$\sqrt{3}$,
∴b=$\frac{3-\sqrt{3}}{2}$,
∴OK=$\frac{3-\sqrt{3}}{2}$.
②如图3中,当OK=OH时,设OK=OH=b,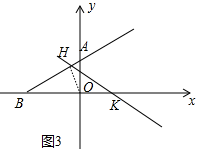
∵∠OHK=∠OKH=∠ABK=30°,
∴∠HOB=60°,
∴∠OHB=90°,
∴OB=2OH
∴2b=$\sqrt{3}$,
∴b=$\frac{\sqrt{3}}{2}$,
∴OK=$\frac{\sqrt{3}}{2}$.
③如图4中,当OK=KH时,设OK=KH=b,作OF⊥AB于F.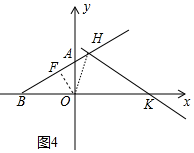
∵∠HBK=∠HKB=30°,
∴HB=KB=OK=b,
在Rt△OBF中,∵OB=$\sqrt{3}$,∠BF0=90°,∠OBF=30°,
∴OF=$\frac{\sqrt{3}}{2}$,BF=$\frac{3}{2}$,
∵∠KOH=∠OHK=75°,∠BHK=120°,
∴∠FHO=45°,
∴FH=OF=$\frac{\sqrt{3}}{2}$,
∴b=BH=BF+FH=$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$,
∴OK=$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$.
综上所述,当△KOH为等腰三角形时,OK的长为$\frac{3-\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$或$\frac{3}{2}$+$\frac{\sqrt{3}}{2}$.
点评 本题考查反比例函数综合题、菱形的性质、直角三角形30度角性质、等腰三角形的判定和性质、三角形的面积等知识,解题的关键是学会利用分割法求 三角形的面积,学会用方程思想思考问题,学会分类讨论,考虑问题要全面,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
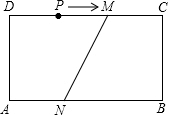 如图,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.点P在CD边上.
如图,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.点P在CD边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
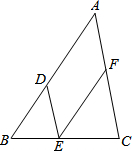 请在下列括号里填上合适的理由:
请在下列括号里填上合适的理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com