
分析 (1)求单价,总价明显,应根据数量来列等量关系.等量关系为:今年的销售数量=去年的销售数量.
(2)关系式为:99≤A款汽车总价+B款汽车总价≤105.
(3)方案获利相同,说明与所设的未知数无关,让未知数x的系数为0即可;多进B款汽车对公司更有利,因为A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,所以要多进B款.
解答 解:(1)设今年4月份A款汽车每辆售价x万元.则:$\frac{80}{x}=\frac{90}{x+1}$,
解得:x=8.
经检验,x=8是原方程的根且符合题意.
答:今年4月份A款汽车每辆售价8万元;
(2)设购进A款汽车y量,则
90≤6.5y+5(15-y)≤96,
解得:10≤y≤14.
因为y的正整数解为10,11,12,13,14,
所以共有5种进货方案;
(3)设总获利为W元,购进A款车辆y辆,则:
W=(8-6.5)y+(7-5-a)(15-y)=(a-0.5)y+30-15a,
当a=0.5时,(2)中所有方案获利相同,
此时,购买A款汽车10辆,B款汽车5辆时对公司更有利.
点评 本题考查分式方程和一元一次不等式组的综合应用,找到合适的等量关系及不等关系是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)
如图,一艘巡逻船在海上A处巡航,突然接到海上指挥中心O处发出的紧急通知,在巡逻船的东北方向的B处有一艘渔船遇险,要马上前去救援,已知点A位于指挥中心O的北偏西60°方向上,且相距60海里,渔船位于指挥中心O的北偏西30°方向上,求A、B两地之间的距离.(结果精确到0.1海里,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{6}$≈2.449)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
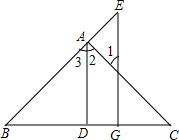 如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:
如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{a}$ | B. | $\sqrt{8{x}^{2}}$ | C. | $\sqrt{{y}^{3}}$ | D. | $\sqrt{\frac{b}{4}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数6.95×105精确到千位 | B. | 3.14是有理数 | ||
| C. | -2$\sqrt{3}<-3\sqrt{2}$ | D. | π-3是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,2∠A+∠B=90°,点0在AB边上,以O点为圆心的圆经过A、C 两点,交AB于D点.
如图,在△ABC中,2∠A+∠B=90°,点0在AB边上,以O点为圆心的圆经过A、C 两点,交AB于D点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C,tan∠BAC=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com