
【题目】如图,点E、A、C在一条直线上,给出下列三个事项:①AD⊥BC, EG⊥BC,垂足分别为D、G;②∠1=∠2;③AD平分∠BAC.

(1)以其中两个事项作为条件,另一个事项作为结论,你能组成 个正确的结论;
(2)请你选择其中一个正确结论进行说明理由.
解:以 为条件, 为结论.(填写序号)
理由是:
【答案】(1)2;(2)①②,③(或①③,②),证明见解析.
【解析】试题分析: (1)首先根据以其中两个事项作为条件,另一个事项作为结论有3种情况,再判断是否都正确,从而得到正确的个数.
(2)根据AD⊥BC, EG⊥BC得到AD∥EG,根据平行线的性质得到∠1=∠CAD, ∠2 =∠BAD,因为∠1=∠2 (或∠CAD=∠BAD),得到∠CAD=∠BAD (∠1=∠2).
试题解析:
(1)2
(2)①②,③(或①③,②)
∵AD⊥BC, EG⊥BC
∴∠ADC =∠EGC=90°
∴AD∥EG
∴∠1=∠CAD, ∠2=∠BAD
∵∠1=∠2 (或∠CAD=∠BAD)
∴∠CAD=∠BAD (∠1=∠2)
∴AD平分∠BAC


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
y | ﹣1 | ﹣0.49 | 0.04 | 0.59 | 1.16 |
那么方程x2+3x﹣5=0的一个近似根是( )
A.1
B.1.1
C.1.2
D.1.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,点A、B分别在直线OM、ON上,BC是∠ABN的平分线.
(1)如图1,若BC所在直线交∠OAB的平分线于点D时,尝试完成①、②两题:
①当∠ABO=30°时,∠ADB= °
②当点A、B分别在射线OM、ON上运动时(不与点O重合),试问:随着点A、B的运动,∠ADB的大小会变吗?如果不会,请求出∠ADB的度数;如果会,请求出∠ADB的度数的变化范围;
(2)如图2, 若BC所在直线交∠BAM的平分线于点C时,将△ABC沿EF折叠,使点C落在四边形ABEF内点C′的位置.求∠BEC′+∠AFC′ 的度数.
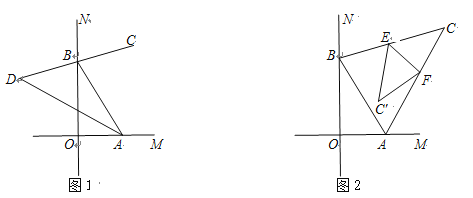
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2x2的图象可以看做抛物线y=2( x-1)2+3怎样平移得到的( )
A.向左平移1个单位,再向下平移3个单位
B.向左平移1个单位,再向上平移3个单位
C.向右平移1个单位,再向上平移3个单位
D.向右平移1个单位,再向下平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把直线y=-x-1沿x轴向右平移2个单位,所得直线的函数解析式为( )
A. y=-x+1B. y=-x-3C. y=-2x-1D. y=2x-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算中,计算正确的是( )
A. 2a3a=6a B. (3a2)3=27a6 C. a4÷a2=2a D. (a+b)2=a2+ab+b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com