
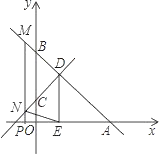
����Ŀ��ֱ��y����x+6��x�ύ��A����y�ύ��B��ֱ��CD��y�ύ��C��0��2����ֱ��AB����D����D��DE��x����E��2��0����
��1����ֱ��CD�ĺ�������ʽ��
��2��P��x����һ���㣬��P��x��Ĵ��ߣ��ֱ���ֱ��AB��CD����M��N����MN�ij�Ϊd��P��ĺ�����Ϊt�����d��t֮��ĺ�����ϵʽ��
��3���ڣ�2���������£���tΪ��ֵʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ���ֱ��д�������
���𰸡���1��ֱ��CD�ĺ�������ʽΪy��x+2����2����t��2ʱ��d����2t+4����t��2ʱ��d��2t��4����3����t��ֵΪ0��4ʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ�
��������
��1���������������D�����꣬�����ô���ϵ���������ֱ��CD�ĺ�������ʽ��
��2����t�ɷֱ��ʾ��M��N�����꣬��ɱ�ʾ��S��t֮��Ĺ�ϵʽ��
��3����������֪MN��DE������ƽ���ı��ε����ʿ�֪MN��DE���ɣ�2���Ĺ�ϵʽ�ɵõ�����t�ķ��̣������t��ֵ��
��1��ֱ��CD��y���ཻ��C��
����ֱ��CD����ʽΪy��kx+2����x��2�����пɵ�y��4��
��D��2��4����
��D����������пɵã�2k+2��4��
��k��1��ֱ��CD�ĺ�������ʽΪy��x+2��
��2�������������֪����OA��t��
��x��t����y����x+6�пɵ�y����t+6
��M��t����t+6����
��x��t����y��x+2�пɵ�y��t+2��
��N��t��t+2����
��t��2ʱ��d����t+6����t+2������2t+4����
��t��2ʱ��d��t+2������t+6����2t��4��
��3���������֪MN��DE��
����M��N��E��DΪ������ı�����ƽ���ı��Σ�
��MN��DE��4��
��|2t��4|��4�����t��0��t��4��
����t��ֵΪ0��4ʱ����M��N��E��DΪ������ı�����ƽ���ı��Σ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ������⣩�ڽ��ʽ����![]() ʱ��С���Ľⷨ���£�
ʱ��С���Ľⷨ���£�
�⣺�������߶�����x��3����2��x����1��2��������é�x����1��2��2�������x����
��1������ΪС������һ�������˴����� ��ֻд��ţ��������ԭ������ ��
��2��С���Ľ��ⲽ����������������ƣ�˵������ȱ����һ�������� ��
��3�������������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У������Խ���AC��BD�ཻ�ڵ�O, ��AOB=60�� AB=4cm.��������ε��ܳ���________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У�AB��CD����D=90�㣬AD=CD=2����E�ڱ�AD�ϣ������A��D�غϣ�����CEB=45�㣬EB��Խ���AC�ཻ�ڵ�F����DE=x��
��1���ú�x�Ĵ���ʽ��ʾ�߶�CF�ij���
��2���������CAE���ܳ�����C��CAE����BAF���ܳ�����C��BAF����![]() =y����y����x�ĺ�����ϵʽ����д�����Ķ�����
=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3������ABE������ֵ��![]() ʱ����AB�ij���
ʱ����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A��ʾ��3����B��ʾ5����C��ʾm.
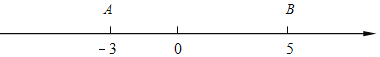
(1)����A���Bͬʱ���������Ḻ�����˶��������ڵ�C����������A���˶��ٶ�Ϊ1��λ����/�룬��B���˶��ٶ�Ϊ3��λ����/�룬��m.
(2)��A��C����֮��ľ���Ϊ2����B��C����֮��ľ���.
(3)��m��0�����������Ƿ����һ��P��ʹP��A��B��C�ľ���͵���12�������ڣ������P��Ӧ�������������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺��32������3��2+3������2��+|��4|
��2�����㣺![]()
��3������5a2+2a��1����4[3��2��4a+a2��]
��4������3x2��[7x����4x��3����2x2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1Ϊij�µ���������ͼ2��![]() �͵Ŀ�ͼ���ҿ�ͼ�����С����������������ÿ��С�����δ�С��ͬ���۲첢˼���������⣺
�͵Ŀ�ͼ���ҿ�ͼ�����С����������������ÿ��С�����δ�С��ͬ���۲첢˼���������⣺
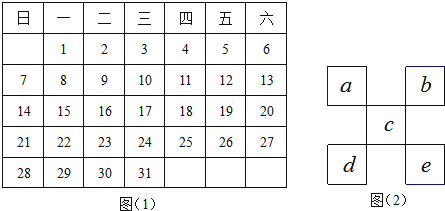
��1����ͼ2��ͼ��������������Ȧ��5���������ڣ�����5�����ĺ͵���Сֵ���� �������ֵ���� ����
��2���ڸ��������п��Եõ��� ���������Ŀ�ͼ��
��3������Ϳ�ͼ��5�����ĺ�Ϊ80����ͼ������ĸa�����������Ƕ��٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����غϵ�������С��ȫ��ͬ�ı߳�Ϊ3��������ABCD��������AB��C��D�䣬��ͼ��ʾ����DAD��=45�㣬��BC��D��C�佻�ڵ�O�����ı���ABOD����ܳ��ǣ�������

A. 6 B. 6![]() C. 3
C. 3![]() D. 3+3
D. 3+3![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
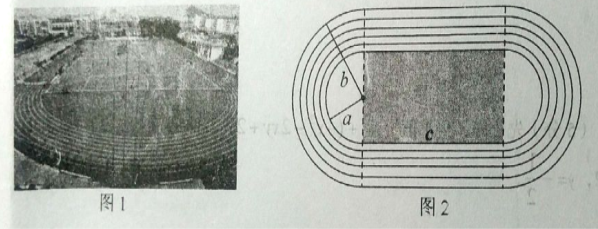
����Ŀ���ۺ���ʵ����
��ͼ1��ijУ�ٳ�ʵ��ͼ��ͼ2�Dzٳ�ʾ��ͼ��ÿ���ܵ�������ֱ���ܵ��������ǰ�Բ�ε��ܵ���ɣ�ÿ�����ܵ�֮��ľ�������ȵģ����ڲ��Բ���ܵ��İ뾶��a�ף�������Բ���ܵ��İ뾶��b�ף�ÿ��ֱ���ij��ȶ���c�ס�
(1)��ʽ��ʾ���ڲ�-Ȧ�ܵ��ij���____.(ֱ��д���𰸣� ��д����)
(2)��ʽ��ʾ�����ٳ���ռ��������___ . (��������ܵ�Ȧס�������ֱ��д���𰸣���д����)
(3)��ѧ�ڣ�ѧУΪ�˸�ѧ�����ṩ������У�����Ͷ������������첢�����ٳ����ܵ��ڲ��ij����β���(ͼ����Ӱ����)��Ƴ������ⲿ�ֵ��������ƺ�����ಿ��(�������ⲿ��������ܵ�֮��IJ���)�����ܽ�.��ȤС����a=35�ף�b=40�ף�c=100�ף� ��ȡ3.����ƺÿƽ��60Ԫ���ܽ�ÿƽ��80Ԫ��������������ƺ���ܽ��ܹ����˶���Ǯ?
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com