
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是城市中某区域的示意图,小聪同学从点O出发,先向西走100米,再向南走200米到达学校,如果学校的位置用(-100,-200)表示,那么(300,200)表示的地点是超市.
如图是城市中某区域的示意图,小聪同学从点O出发,先向西走100米,再向南走200米到达学校,如果学校的位置用(-100,-200)表示,那么(300,200)表示的地点是超市.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
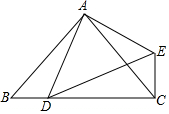 将两块大小不同的等腰直角三角板△ABC与△ADE(其中∠BAC=∠DAE=90°)按如图位置摆放,使点D恰好落在BC边上,求证:BD=CE.
将两块大小不同的等腰直角三角板△ABC与△ADE(其中∠BAC=∠DAE=90°)按如图位置摆放,使点D恰好落在BC边上,求证:BD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com