
����Ŀ������������ֱ��������2��1����3����4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ���������ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm�����������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1���뻭����״ͼ��д����m��n�����п��ܵĽ����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������ĸ��ʣ�
���𰸡�
��1���⣺����״ͼ�ã�

��m��n������12�ֵȿ��ܵĽ������2��1������2����3������2����4������1��2������1����3������1����4��������3��2��������3��1��������3����4��������4��2��������4��1��������4����3��
��2���⣺����ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڵڶ��������������У�����3����4��������4����3����
����ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڵڶ������������ĸ���Ϊ�� ![]() =
= ![]()
����������1���¼�����������ɣ���һ����4���������2����3�֣�����4![]() 3=12�֣���2��ͼ���ڶ�������������Ҫ��m<0,,n<0,��2�֣������������.
3=12�֣���2��ͼ���ڶ�������������Ҫ��m<0,,n<0,��2�֣������������.
�����㾫����������Ĺؼ�����������ʹ�ʽ�����֪ʶ������һ��أ������һ�������У���n�ֿ��ܵĽ�����������Ƿ����Ŀ����Զ���ȣ��¼�A�������е�m�н������ô�¼�A�����ĸ���ΪP��A��=m/n��


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��
��1����֤��![]() ��
��
��2����![]() ����
����![]() �Ķ�����
�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O���ң�DΪOA�뾶���е㣬��D��CD��OA����AB�ڵ�E������O�ڵ�F����CE=CB��
��1����֤��BC�ǡ�O�����ߣ�
��2������AF��BF�����ABF�Ķ�����
��3�����BE=10��sinA= ![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB=90�㣬��A�Ƶ�O˳ʱ����ת��Ķ�Ӧ��A1��������OB�ϣ���A�Ƶ�A1˳ʱ����ת��Ķ�Ӧ��A2��������OB�ϣ���A�Ƶ�A2˳ʱ����ת��Ķ�Ӧ��A3��������OB�ϣ���������AA1 �� AA2 �� AA3�����������������AAnAn+1�����ȣ����ú�n�Ĵ���ʽ��ʾ��nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��,
��,![]() ,��
,��![]() ��
��![]() ƽ�ƣ���ʹ
ƽ�ƣ���ʹ![]() ��ƽ�Ƶ�
��ƽ�Ƶ�![]() ��,
��,![]() ƽ�ƺ�Ķ�Ӧ��ֱ�Ϊ
ƽ�ƺ�Ķ�Ӧ��ֱ�Ϊ![]() ��
��

��1���![]() ���������;
���������;
��2������ƽ�ƺ����õ�![]() ;
;
��3�������![]() �����
�����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���![]() ���������㣺
���������㣺![]()
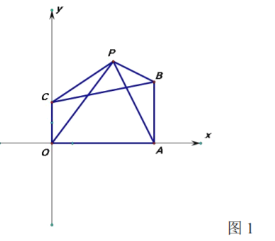
��1�������![]() ������
������
��2����ͼ1������![]() ����
����![]() ���ı���
���ı���![]() �������ڵ�һ���ޣ�����
�������ڵ�һ���ޣ�����![]() ����
����![]() ����
����![]() �����꣮
�����꣮
��3����ͼ2��ʾ��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬
��һ���㣬![]() ����
����![]() �ҲࣩΪ
�ҲࣩΪ![]() ��һ���㣬ʹ
��һ���㣬ʹ![]() ��ʼ��ƽ��
��ʼ��ƽ��![]() ����
����![]() ��
��![]() ����ô
����ô![]() �Ƿ�Ϊ��ֵ����Ϊ��ֵ����ֱ��д����ֵ�������ǣ����˵�����ɣ�
�Ƿ�Ϊ��ֵ����Ϊ��ֵ����ֱ��д����ֵ�������ǣ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������С����ܼ��ţ���̼���á����ߺ������������Ƚϳ�����ij���������̹���A��B�����ͺŵĵ���������������A�������Ľ������۱�B�������Ľ������۶�2��Ԫ��50��Ԫ����A�������������뻨40��Ԫ����B��������������ͬ�������з���A��������ÿ������yA��̨�����ۼ�x����Ԫ/̨�����㺯����ϵʽyA=��x+20��B��������ÿ������yB��̨�����ۼ�x����Ԫ/̨�����㺯����ϵʽyB=��x+14��
��1����A��B�����ͺŵ������Ľ������ۣ�
��2����֪A���������ۼ۱�B���������ۼ۸�2��Ԫ/̨����B�������ۼ�Ϊt��Ԫ/̨��ÿ�����������ֳ���������ΪW��Ԫ����W��t�ĺ�����ϵʽ��A��B�����ͺŵ������ۼ۸�Ϊ����ʱ��ÿ�����������ֳ����������������������Ƕ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֤����
��֪����ͼ���� D��E��F �ֱ����߶� AB��BC��AC �ϣ����� DE��EF��DM ƽ�֡�ADE �� EF �ڵ� M����1+��2=180���� ��֤����B =��BED��
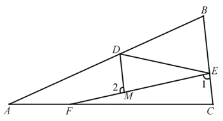
֤�����ߡ�1+��2=180������֪����
���ߡ�1+��BEM=180����ƽ�Ƕ��壩��
���2=��BEM�� ����
��DM�� �� ����
���ADM =��B�� ����
��MDE =��BED�� ����
����DM ƽ����ADE (��֪)��
���ADM =��MDE (��ƽ���߶���)��
���B =��BED�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4�������16����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F��![]() ����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��
����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��![]() �ܳ�����СֵΪ
�ܳ�����СֵΪ![]() ����
����![]()

A. 6 B. 8 C. 10 D. 12
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com