
分析 (1)分别求出两方程的根,根据定义判断即可;
(2)可先假设互为“共轭方程”,令方程x2+2mx+n=0的两根为p、q,则方程x2-6x-n=0的两根为p、-q,由韦达定理可得p+q=-2m,pq=n,p-q=6,将其代入(p+q)2-4pq=(p-q)2可得m、n间需要满足的关系,从而做出判断.
解答 解:(1)不是,
解方程x2+x-12=0可得:x1=3,x2=-4,
解方程x2-x-12=0可得:x3=-3,x4=4,
∵x1≠x3,
∴方程x2+x-12=0与x2-x-12=0不是“共轭方程”;
(2)存在,
假设方程x2+2mx+n=0与x2-6x-n=0互为“共轭方程”,
令方程x2+2mx+n=0的两根为p、q,
则方程x2-6x-n=0的两根为p、-q,
根据题意可知,p+q=-2m,pq=n,p-q=6,
由(p+q)2-4pq=(p-q)2,可得4m2-4n=36,即n=m2-9
∴对于任意实数m,当存在实数n(n≥-9)时,两方程互为“共轭方程”.
点评 本题主要考查一元二次方程根与系数的关系,理解新定义并熟练掌握韦达定理是解题的关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
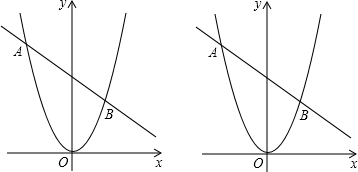
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
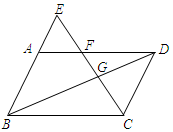 如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,交BD于点G,AE:AB=1:3,设$\overrightarrow{BA}$=$\overrightarrow a$,$\overrightarrow{BC}$=$\overrightarrow b$.
如图,E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F,交BD于点G,AE:AB=1:3,设$\overrightarrow{BA}$=$\overrightarrow a$,$\overrightarrow{BC}$=$\overrightarrow b$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
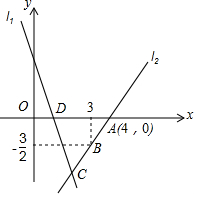 如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D.直线l2经过点A、B,直l1,l2交于点C.
如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D.直线l2经过点A、B,直l1,l2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 日期 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 | 11日 |
| 加油量(升) | +100 | -300 | -200 | -100 | +1000 | -1200 | -100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com