
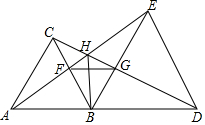
 如图,△ABC和△BDE都是等边三角形,A、B、D三点共线.
如图,△ABC和△BDE都是等边三角形,A、B、D三点共线.分析 由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
解答 解:∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,$\left\{\begin{array}{l}{AB=BC}&{\;}\\{∠ABE=∠CBD}&{\;}\\{BE=BD}&{\;}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴在△BGD和△BFE中,$\left\{\begin{array}{l}{∠DBG=∠FBE}&{\;}\\{BD=BE}&{\;}\\{∠BDC=∠AEB}&{\;}\end{array}\right.$,
∴△BGD≌△BFE(ASA),
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
在△ABF和△CGB中,$\left\{\begin{array}{l}{BF=BG}&{\;}\\{∠ABF=∠CBG=60°}&{\;}\\{AB=BC}&{\;}\end{array}\right.$,
∴△ABF≌△CGB(SAS),
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∴①②③④⑤都正确.
故答案为:①②③④⑤.
点评 本题主要考查了等边三角形的性质及全等三角形的判定及性质等知识;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1<mx-n的解集为( )
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1<mx-n的解集为( )| A. | x<m | B. | x<2 | C. | x<1 | D. | x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
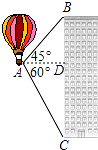 热气球的探测器显示,从热气球A看一栋楼顶部B的仰角α为45°,看这栋楼底部C的俯角β为60°,热气球与楼的水平距离为100m,求这栋楼的高度(结果保留根号).
热气球的探测器显示,从热气球A看一栋楼顶部B的仰角α为45°,看这栋楼底部C的俯角β为60°,热气球与楼的水平距离为100m,求这栋楼的高度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
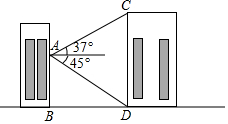 如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)
如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com