
【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
⑴二次函数y=ax2+bx+c有最小值,最小值为﹣3;
⑵当 ![]() 时,y<0;
时,y<0;
⑶二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是( )
A.3
B.2
C.1
D.0
【答案】B
【解析】解;由表格数据可知,二次函数的对称轴为直线x=1,
所以,当x=1时,二次函数y=ax2+bx+c有最小值,最小值为﹣4;故(1)小题错误;
根据表格数据,当﹣1<x<3时,y<0,
所以,﹣ ![]() <x<2时,y<0正确,故(2)小题正确;
<x<2时,y<0正确,故(2)小题正确;
二次函数y=ax2+bx+c的图象与x轴有两个交点,分别为(﹣1,0)(3,0),它们分别在y轴两侧,故(3)小题正确;
综上所述,结论正确的是(2)(3)共2个.
故选B.
【考点精析】根据题目的已知条件,利用二次函数的最值和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】某运输公司用10辆相同的汽车将一批苹果运到外地,每辆汽车能装8吨甲种苹果,或10吨乙种苹果,或11吨丙种苹果.公司规定每辆车只能装同一种苹果,而且必须满载.已知公司运送了甲、乙、丙三种苹果共100吨,且每种苹果不少于一车.
(1)设用x辆车装甲种苹果,y辆车装乙种苹果,求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若运送三种苹果所获利润的情况如下表所示:

设此次运输的利润为W(万元),问:如何安排车辆分配方案才能使运输利润W最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
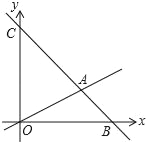
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
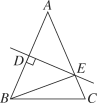
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,交AB于点D.
(1)若∠A=40°,求∠CBE的度数;
(2)若△BCE的周长为8cm,AB=5cm,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的长方体.
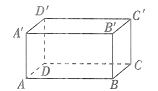
(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
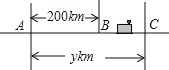
【题目】如图,A、B两地相距200km,一列火车从B地出发沿BC方向以![]() 的速度行驶,在行驶过程中,这列火车离A地的路程
的速度行驶,在行驶过程中,这列火车离A地的路程![]() 与行驶时间
与行驶时间![]() 之间的函数关系式是______.
之间的函数关系式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级学生参加夏令营,已知:用3辆小客车和1辆大客车每次可运送学生105人;用一辆小客车和2辆大客车每次可运送学生110人,现有学生400人,计划租用小客车a辆,大客车b辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可送多少名学生?
(2)请你帮学校设计出所有的租车方案;
(3)若小客车每辆需租金200元,大客车每辆需租金380元,请选出最省钱的方案,并求出最省租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).
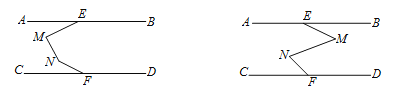
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com