Question

3．操作与证明：

如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．
（1）连接AE，求证：△AEF是等腰三角形；
猜想与发现：
（2）在（1）的条件下，请判断线段MD与MN的关系，得出结论；
结论：DM、MN的关系是：DM=MN，DM⊥MN；
拓展与探究：
（3）如图2，将图1中的直角三角板ECF绕点C旋转180°，其他条件不变，则（2）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

Answer 1

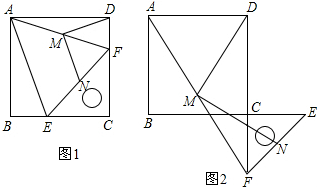
分析 （1）欲证明△AEF是等腰三角形，只要证明△ABE≌△ADF即可；
（2）结论：DM=MN，DM┴MN．利用三角形中位线定理．直角三角形斜边中线定理即可解决问题．
（3）结论不变．证明方法类似．

解答 （1）证明：如图1中，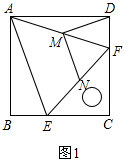

∵四边形ABCD是正方形，
∴AB=BC=CD=AD，∠B=∠ADF=90°，
∵CE=CF，
∴BE=DF，
∴△ABE≌△ADF，
∴AE=AF，
∴△AEF是等腰三角形．

（2）解：结论：DM=MN，DM┴MN
证明：∵AM=FM，FN=EN，
∴MN=$\frac{1}{2}$AE，DM=$\frac{1}{2}$AF，
∵AE=AF，
∴MN=DM，
∵∠ADF=90°，AM=MF，
∴MD=MA=MF，
∴∠MAD=∠ADM，
∵∠DMF=∠MAD+∠ADM=2∠DAM，
∵△ABE≌△ADF，
∴∠BAE=∠DAF，
∵∠EAF+2∠DAM=90°，
∵MN∥AE，
∴∠NMF=∠EAF，
∴∠NMF+∠DMF=90°，
∴DM⊥MN．
∴MN=DM，MN⊥DM．
故答案为MN=DM，MN⊥DM．

（3）解：结论仍然成立．
理由：如图2中，连接AE，设AE交DM于O，交CD于G．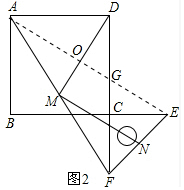

∵AB=AD，BE=DF，∠ABE=∠ADF=90°，
∴△ABE≌△ADF，
∴AF=AE，∠AFD=∠AEB，
∵AM=MF，FN=EN，
∴MN=$\frac{1}{2}$AE，DM=$\frac{1}{2}$AF，
∴MN=DM，
∵DM=MF=AM，
∴∠MDF=∠MFD=∠AEB，
∵∠DGO=∠CGE，∠ODG=∠CEG，
∴∠DOG=∠ECG=90°，
∵NM∥AE，
∴∠DOG=∠DMN=90°，
∴MN⊥DM，MN=DM．

点评 本题考查四边形综合题、全等三角形的判定和性质、三角形中位线定理、直角三角形斜边中线定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考压轴题．