
 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}+3}{2}$ | C. | $\frac{\sqrt{3}+3}{4}$ | D. | $\frac{3\sqrt{3}+3}{4}$ |
分析 先证△AOE′≌△BOF′得∠OAE′=∠OBF′,即可知∠CPB=∠AOC=90°,得点P、B、A、O四点共圆,由当点P在劣弧OB上运动时,点P的纵坐标随着∠PAO的增大而增大,找到使点P的纵坐标最大时点P的位置(点P与点D′重合时),然后运用勾股定理及30°角所对的直角边等于斜边的一半等知识即可求出点P的纵坐标的最大值.
解答 解:如图1,
∵正方形OE′D′F′是由正方形OEDF绕点O顺时针旋转所得,
∴∠AOE′=∠BOF′.
在△AOE′和△BOF′中,
∵$\left\{\begin{array}{l}{AO=BO}\\{∠AOE′=∠BOF′}\\{OE′=OF′}\end{array}\right.$,
∴△AOE′≌△BOF′(SAS).
∴∠OAE′=∠OBF′.
∵∠ACO=∠BCE′,
∴∠CPB=∠AOC=90°
∴点P、B、A、O四点共圆,
∴当点P在劣弧OB上运动时,点P的纵坐标随着∠PAO的增大而增大.
∵OE′=$\frac{3}{2}$,
∴点E′在以点O为圆心,$\frac{3}{2}$为半径的圆O上运动,
∴当AP与⊙O相切时,∠E′AO(即∠PAO)最大,
此时∠AE′O=90°,点D′与点P重合,点P的纵坐标达到最大.
过点P作PH⊥x轴,垂足为H,如图2所示.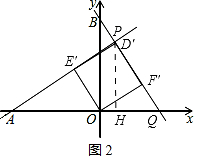
∵∠AE′O=90°,E′O=$\frac{3}{2}$,AO=3,
∴∠E′AO=30°,AE′=$\frac{3\sqrt{3}}{2}$.
∴AP=$\frac{3\sqrt{3}+3}{2}$.
∵∠AHP=90°,∠PAH=30°,
∴PH=$\frac{1}{2}$AP=$\frac{3\sqrt{3}+3}{4}$.
∴点P的纵坐标的最大值为$\frac{3\sqrt{3}+3}{4}$,
故选:D.
点评 本题是在图形旋转过程中,考查了全等三角形的判定与性质、勾股定理、30°角所对的直角边等于斜边的一半等知识,而找到使点P的纵坐标最大时点P的位置是解决最后一个问题的关键.


科目:初中数学 来源: 题型:填空题
| 移植的棵数n | 300 | 700 | 1000 | 5000 | 15000 |
| 成活的棵数m | 280 | 622 | 912 | 4475 | 13545 |
| 成活的频率$\frac{m}{n}$ | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
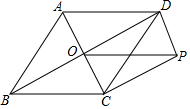 如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.
如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=4,DP∥AC,CP∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
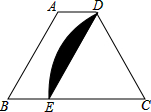 如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.
如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
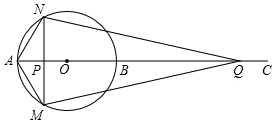 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com