
分析 先把$\sqrt{a-5}$+b2-6b+9=0,配方得出$\sqrt{a-5}$+(b-3)2=0,求出a,b的值,再根据三角形的三边关系,求出c的取值范围,即可得出△ABC的周长取值范围.
解答 解:∵$\sqrt{a-5}$+b2-6b+9=0,
∴$\sqrt{a-5}$+(b-3)2=0,
∵$\sqrt{a-5}$≥0,(b-3)2≥0,
∴a-5=0,b-3=0,
∴a=5,b=3,
∵△ABC的三边为a,b,c,
∴b-a<c<b+a,即5-3<c<5+3,
∴c的取值范围为:2<c<8,
∴2+5+3<c+a+b<8+5+3,
即10<△ABC的周长<16,
故答案为:10<△ABC的周长<16.
点评 此题考查了配方法的应用,用到的知识点是配方法、三角形的三边关系,关键是通过配方求出a,b的值.三角形两边之和大于第三边,三角形的两边差小于第三边.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
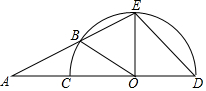 如图,CD是半圆的直径,O为圆心,E是半圆上一点,且∠EOD=93°,A是DC延长线上一点,AE与半圆相交于点B.若AB=OC,则∠EAD=31°,∠EOB=56°.
如图,CD是半圆的直径,O为圆心,E是半圆上一点,且∠EOD=93°,A是DC延长线上一点,AE与半圆相交于点B.若AB=OC,则∠EAD=31°,∠EOB=56°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
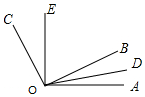 如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.
如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
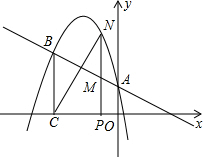 二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
二次函数y=ax2+bx+c的图象经过点(-1,4),且与直线y=-$\frac{1}{2}$x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com