
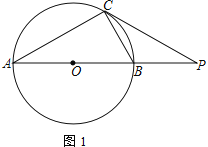
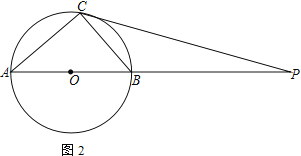
【题目】如图,⊙O为Rt△ACB的外接圆,点P是AB延长线上的一点,PC切⊙O于点C,连AC
(1)若AC=CP,求![]() 的值
的值
(2)若sin∠APC=![]() ,求tan∠ABC
,求tan∠ABC
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)连接OC,根据已知条件易证△ACO≌△PCB(AAS),根据全等三角形的性质可得OC=BC=OB,可判定△OBC为等边三角形,即求得结论;(2)连接OC,先证△PCB∽△PAC,根据相似三角形的性质可得![]() ,再求得PC的长,即可求得结论.
,再求得PC的长,即可求得结论.
试题解析:
(1)∵AC=CP
∴∠A=∠P
连接OC
∵PC切⊙O于点C
∴∠OCP=90°
∵∠ACB=90°
∴∠ACO=∠PCB
在△ACO和△PCB中

∴△ACO≌△PCB(AAS)
∴OC=BC=OB
∴△OBC为等边三角形
∴∠OBC=60°,∠A=∠P=30°
∴![]()
(2) 连接OC,
∵PC切于点C
∴∠OCP=90°
∴∠PCB+∠OCB=90°
∵∠ACB=90°
∴∠CAB+∠CBA=90°
∵OB=OC
∴∠OBC=∠OCB
∴∠PCB=∠PAC
∴△PCB∽△PAC
∴![]()
∵sin∠APC=![]()
∴设OC=7,OP=25,则OB=OA=7,BP=18
∴![]()
∴PC=12
∴tan∠ABC=![]()



科目:初中数学 来源: 题型:
【题目】某学校校门口有一个长为9m的长条形(长方形)电子显示屏,学校的有关活动都会在“电子显示屏”播出,由于各次活动的名称不同,字数也就不等,为了制作及显示时方便美观,负责播出的老师对有关数据作出了如下规定:若字数在8个以下,边空:字宽:字距=2:4:1;若字数在8个以上(含8个),边空:字宽:字距=2:3:1,如图所录:
(1)某次活动的字数为9个,求字距是多少?
(2)如果某次活动的字宽为36cm,问字数是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
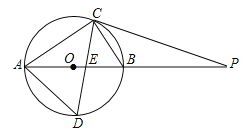
【题目】如图,AB为⊙O的直径,C为⊙O上一点,D、E分别是∠ACB的平分线与⊙O、AB的交点,P为AB延长线上一点,且PC=PE.试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H. 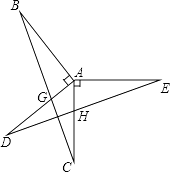
求证:
(1)△ABC≌△ADE;
(2)BC⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
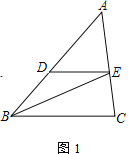
【题目】△ABC中,D、E分别为AB、AC边上的点,DE∥BC,连接BE
(1)如图1,已知AB=6,AC=5,BC=4.若∠DBE=∠EBC,求DE的长
(2)如图2,F为BC的中点,连接DF交BE于G,连接AG交BC于H,求![]() 的值
的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个;B.4个;C.5个;D.6个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( ) 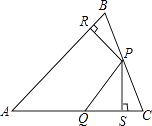
A.①②③
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的括号里:
﹣8,0.275, ![]() ,0,﹣1.04,﹣(﹣3),﹣
,0,﹣1.04,﹣(﹣3),﹣ ![]() ,|﹣2|
,|﹣2|
正数集合{…}
负整数集合{…}
分数集合{…}
负数集合{…}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com