
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

【答案】![]() ,
,![]() ,
,![]() ,
,![]() ;
;
【解析】
题中没指明△ODP的腰长与底分别是哪个边,故应该分情况进行分析,从而求得点P的坐标.
(1)OD是等腰三角形的底边时,此时P(2.5,4);
(2)OD是等腰三角形的一条腰时:
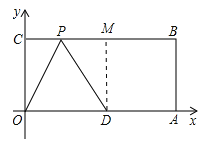
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,在直角OPC中,CP=![]() =
=![]() =3,则P的坐标是(3,4);②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,过D作DM⊥BC于点M,在直角PDM中,PM=
=3,则P的坐标是(3,4);②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,过D作DM⊥BC于点M,在直角PDM中,PM=![]() =3,当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4);故P的坐标为: (2.5,4);(3,4); (2,4)或(8,4).
=3,当P在M的左边时,CP=5-3=2,则P的坐标是(2,4);当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4);故P的坐标为: (2.5,4);(3,4); (2,4)或(8,4).
故答案为: (2.5,4);(3,4);(2,4)或(8,4)


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方。即如果一个直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么
,那么![]() 。
。
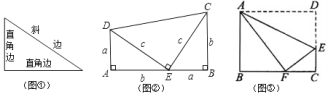
(1)直接填空:如图①,若a=3,b=4,则c= ;若![]() ,
,![]() ,则直角三角形的面积是 ______ 。
,则直角三角形的面积是 ______ 。
(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明![]() 。
。
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
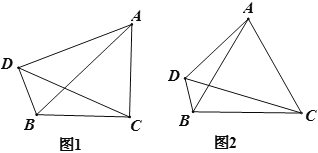
【题目】已知:在△ABC中,AC=BC,点D在△ABC外部,且∠ACB+∠ADB=180°,连接AB、CD.
(1)如图1,当∠ACB=90°时,则∠ADC=______°.
(2)如图2,当∠ACB=60°时,求证:DC平分∠ADB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)
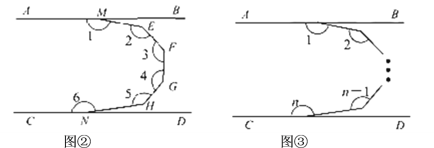
(1)如图①,已知 AB ∥CD,求证 :∠1+∠MEN+∠2=360°

(推广应用)
(2)如图②,已知 AB∥ CD,求∠1+∠2+∠3+∠4+∠5 +∠6的度数为___________.
如图③,已知 AB∥CD ,求∠1+∠2+∠3+∠4+∠5 +∠6+…+∠n的度数为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种铂金饰品在甲、乙两种商店销售,甲店标价每克468元,按标价出售,不优惠,乙店标价每克525元,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.若购买的铂金饰品重量为![]() 克,其中
克,其中![]() .
.
(1)分别列出到甲、乙商店购买该种铂金饰品所需费用(用含x的代数式表示);
(2)李阿姨要买一条重量10克的此种铂金饰品,到哪个商店购买最合算;
(3)要买一条重量多少克的此种铂金饰品,才能到乙商店购买比到甲商店优惠300元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=60°,∠C=40°,DE垂直平分BC,连接BD.
(1)尺规作图:过点D作AB的垂线,垂足为F.(保留作图痕迹,不写作法)
(2)求证:点D到BA,BC的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com