
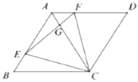
【题目】已知菱形![]() ,
,![]() 是动点,边长为4,
是动点,边长为4,![]() ,则下列结论正确的有几个( )
,则下列结论正确的有几个( )
①![]() ; ②
; ②![]() 为等边三角形
为等边三角形
③![]() ④若
④若![]() ,则
,则![]()
A.1B.2C.3D.4
【答案】D
【解析】
①易证△ABC为等边三角形,得AC=BC,∠CAF=∠B,结合已知条件BE=AF可证△BEC≌△AFC;②得FC=EC,∠FCA=∠ECB,得∠FCE=∠ACB,进而可得结论;③证明∠AGE=∠BFC则可得结论;④分别证明△AEG∽△FCG和△FCG∽△ACF即可得出结论.
在四边形![]() 是菱形中,
是菱形中,
∵![]() ,
,
∴![]()
∵![]()
∴![]()
∴△ABC为等边三角形,
∴![]()
又![]() ,
,
∴![]() ,故①正确;
,故①正确;
∴![]() ,
,![]()
∴∠FCE=∠ACB=60°,
∴![]() 为等边三角形,故②正确;
为等边三角形,故②正确;
∵∠AGE+∠GAE+∠AEG=180°,∠BEC+∠CEF+∠AEG=180°,
又∵∠CEF=∠CAB=60°,
∴∠BEC=∠AGE,
由①得,∠AFC=∠BEC,
∴∠AGE=∠AFC,故③正确;
∴∠AEG=∠FCG
∴△AEG∽△FCG,
∴![]() ,
,
∵∠AGE=∠FGC,∠AEG=∠FCG
∴∠CFG=∠GAE=∠FAC,
∴△ACF∽△FCG,
∴![]()
∴![]()
∵AF=1,
∴BE=1,
∴AE=3,
∴![]() ,故④正确.
,故④正确.
故选D.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
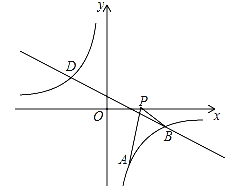
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:


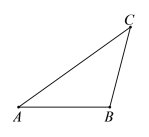
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接OA,OB,OC,
由作图可知 OA=OB=OC( )(填推理的依据)
∴⊙O为△ABC的外接圆;
∵点C,P在⊙O上,![]()
∴∠APB=∠ACB.( )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
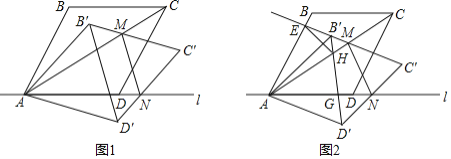
【题目】图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.
(1)当MN∥B′D′时,求α的大小.
(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆(吊杆垂直于桥面),把桥面吊住.某悬索桥(如图1),是连接两个地区的重要通道. 图2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引. 他通过查找资料了解到此桥的相关信息:这座桥的缆索(即图2中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即AB=CD, 两个索塔均与桥面垂直. 主桥AC的长为600 m,引桥CE的长为124 m.缆索最低处的吊杆MN长为3 m,桥面上与点M相距100 m处的吊杆PQ长为13 m.若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端D与锚点E的距离.


图2
查看答案和解析>>
科目:初中数学 来源: 题型:
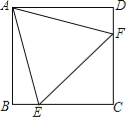
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.

(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)该运动员身高1.7米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?.
查看答案和解析>>
科目:初中数学 来源: 题型:
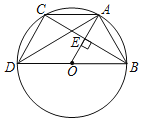
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,∠BAC=120°、OA⊥BC、若AB=4.
(1)求证:四边形OACD为菱形.
(2)求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com