
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)N(3,0);(3)OM=
x+4;(2)N(3,0);(3)OM=![]() AC.
AC.
【解析】
试题分析:(1)由B、C的坐标,利用待定系数法可求得抛物线解析式;
(2)可设N(n,0),则可用n表示出△ABN的面积,由NM∥AC,可求得![]() ,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
,则可用n表示出△AMN的面积,再利用二次函数的性质可求得其面积最大时n的值,即可求得N点的坐标;
(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得OM=![]() AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
AB,在Rt△AOB和Rt△AOC中,可分别求得AB和AC的长,可求得AB与AC的关系,从而可得到OM和AC的数量关系.
试题解析:(1)将点B,点C的坐标分别代入y=ax2+bx+4可得
![]() ,
,
解得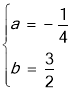 ,
,
∴二次函数的表达式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)设点N的坐标为(n,0)(﹣2<n<8),
则BN=n+2,CN=8﹣n.
∵B(﹣2,0),C(8,0),
∴BC=10,
在y=﹣![]() x2+
x2+![]() x+4中,令x=0,可解得y=4,
x+4中,令x=0,可解得y=4,
∴点A(0,4),OA=4,
∴S△ABN=![]() BNOA=
BNOA=![]() (n+2)×4=2(n+2),
(n+2)×4=2(n+2),
∵MN∥AC,
∴![]()
∴![]() ,
,
∴![]()
∵﹣![]() <0,
<0,
∴当n=3时,即N(3,0)时,△AMN的面积最大;
(3)当N(3,0)时,N为BC边中点,
∵MN∥AC,
∴M为AB边中点,
∴OM=![]() AB,
AB,
∵AB=![]() ,AC=
,AC=![]() ,
,
∴AB=![]() AC,
AC,
∴OM=![]() AC.
AC.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H. 
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG= ![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程,并解答后面的问题:
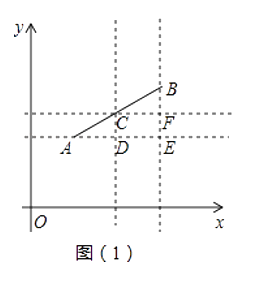
如图1,在平面直角坐标系xOy中,A(x1 , y1),B(x2 , y2),C为线段AB的中点,求C点的坐标.
解:分布过A、C做x轴的平行线,过B、C做y轴的平行线,两组平行线的交点如图1所示.
设C(x0 , y0),则D(x0 , y1),E(x2 , y1),F(x2 , y0)
由图1可知:x0= ![]() =
= ![]()
y0= ![]() =
= ![]()
∴( ![]() ,
, ![]() )
)
问题:
(1)已知A(﹣1,4),B(3,﹣2),则线段AB的中点坐标为
(2)平行四边形ABCD中,点A、B、C的坐标分别为(1,﹣4),(0,2),(5,6),求点D的坐标.
(3)如图2,B(6,4)在函数y= ![]() x+1的图象上,A(5,2),C在x轴上,D在函数y=
x+1的图象上,A(5,2),C在x轴上,D在函数y= ![]() x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.
x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.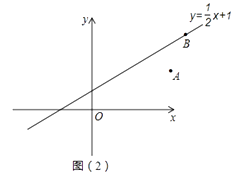
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,动点P从点A开始沿A→B→C→D的路径匀速运动到点D为止,在这个过程中,下列图象可以大致表示△APD的面积S随点P的运动时间t的变化关系的是( )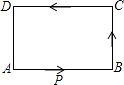
A.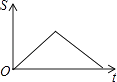
B.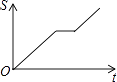
C.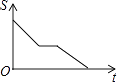
D.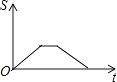
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com