
分析 根据有理数的加减混合运算法则计算即可.
解答 解:(1)(-6)-(+6)-(-7)=-6-6+7=-5;
(2)0-(+8)+(-27)-(+5)=-8-27-5=-40;
(3)(-$\frac{2}{3}$)+(+0.25)+(-$\frac{1}{6}$)-(+$\frac{1}{2}$)=-$\frac{2}{3}$-$\frac{1}{6}$-$\frac{1}{2}$+$\frac{1}{4}$=-$\frac{4}{3}$+$\frac{1}{4}$=-$\frac{13}{12}$;
(4)(+3$\frac{3}{5}$)+(4$\frac{3}{4}$)-(+1$\frac{2}{5}$)+(-3$\frac{3}{4}$)=3$\frac{3}{5}$-1$\frac{2}{5}$+4$\frac{3}{4}$-3$\frac{3}{4}$=2$\frac{1}{5}$+1=3$\frac{1}{5}$.
点评 本题考查的是有理数的加减混合运算,掌握有理数的加减混合运算法则是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
如图,在热气球上A处测得一栋大楼顶部B的俯角为23°,测得这栋大楼底部C的俯角为45°.已知热气球A处距地面的高度为180m,求这栋大楼的高度(精确到1m).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
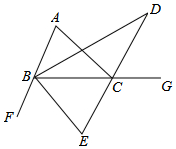 如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.
如图,∠CBF、∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC、∠CBF的平分线BD、BE交于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
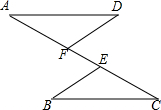 如图,已知AE=CF,AD=BC,DF=BE.
如图,已知AE=CF,AD=BC,DF=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
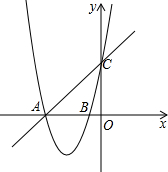 如图,抛物线经过A(-2,0),B(-$\frac{1}{2}$,0),C(0,2)三点.
如图,抛物线经过A(-2,0),B(-$\frac{1}{2}$,0),C(0,2)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
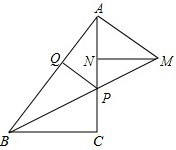 如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.
如图,已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN,NP=2,PC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.
如图,已知四边形ABCD,其中A(1,1),B(2,2),C(0,3),D(-3,0),作出四边形ABCD关于原点对称的四边形A′B′C′D′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com